Força Elástica Exercícios Resolvidos-1

EX-01 (UFRJ - 2007)

Um bloco de massa 5 kg está parado sobre um plano inclinado de um ângulo de 30° com a horizontal, preso a uma mola, de constante elástica k = 100 N/m, como mostra a figura. O atrito entre o bloco e o plano pode ser desprezado.

a) Represente as forças que atuam na caixa e escreva quem exerce cada uma das forças.

b) Calcule a deformação da mola nessa situação.

Solução:

Calculando a deformação x da mola:

Dados: m = 5 kg; k = 100 N/m

Adotar: g = 10 m/s²

Se F_M = Psen30º → k.x = m.g.1/2 → 100.x = 5.10.1/2 → x = 0,25 m →

x = 25 cm

EX-02 (UFB)

Entre dois blocos 1 e 2 de massas m₁=12 kg e m₂=8 kg existe uma mola ideal A. Os dois blocos estão apoiados sobre

um plano horizontal sem atrito. O bloco 1 é puxado por uma força F constante, horizontal e paralela ao plano por meio de outra mola ideal B, idêntica à mola A. Calcule a relação x_A/x_B entre as deformações das molas A e B, depois que o sistema entrou em movimento com aceleração constante a.

Solução:

EX-03 (UFPE 2005)

Duas molas A e B de comprimentos iguais a L, mas de constantes elásticas diferentes ( K_A = 0,2 K_B ), são unidas no ponto C e alongadas até o comprimento total 4L. Os terminais das molas são então fixados em suportes rígidos, como mostra a figura. Determine a razão, L_A/L_B entre os comprimentos das molas nessa situação

Solução:

Dados:

K_A = 0,2 K_B

L_A + L_B = 4L

Temos que:

L_A = L + x_A  (sendo x_A  é a deformação da mola A)

L_B = L + x_B  (sendo x_B  é a deformação da mola B)

E como o ponto C está em equilíbrio, tem-se:

K_A.x_A = K_B.x_B  →  0,2K_B.x_A=K_B.x_B  →  x_A = 5.x_B  (1)

L_A + L_B = 4L →  (L + x_A) + (L + x_B) = 4L →  2L + x_A + x_B = 4L →

x_A + x_B = 2L (2)

(1) em (2) → 5.x_B  + x_B = 2L →  6.x_B = 2L  →  x_B = 1.L/3

Logo, x_A = 5.x_B  → x_A = 5L/3

Portanto,

EX-04 (UFSM)

Durante os exercícios de força realizados por um corredor, é usada uma tira de borracha presa ao seu abdome. Nos arranques, o atleta obtém os seguintes resultados:

O máximo de força atingido pelo atleta, sabendo-se que a constante elástica da tira é de 300 N/m e que obedece à lei de Hooke, é, em N,

a) 23520       b) 17600        c) 1760       d) 840        e) 84

Solução:

Lei de Hooke:  F_elástico = K.∆x, portanto, a força é máxima para ∆x máximo.

Logo,

F_max = K.∆x → F_max = 300.0,28 = 84 →  F_max = 84 N

Resposta: alternativa e

EX-05 (Mackenzie-SP)

A mola da figura varia seu comprimento de 10cm para 22cm quando penduramos em sua extremidade um corpo de 4N. 

Determine o comprimento total dessa mola quando penduramos nela um corpo de 6N.

Solução:

A deformação da mola para carga de 4 N foi de ∆x = 22 – 10 = 12 cm.

Logo, podemos calcular a constante de mola K:

F=K.∆x → 4 = K.0,12 → K = 100/3 N/m

Portanto, a deformação para uma carga de 6 N será:

F’=K.∆x’ → 6 = 100/3. ∆x’ → ∆x’ = 0,18 m  →  ∆x’ = 18 cm 

Logo, o comprimento total da mola é:

L = 10 + 18 = 28 cm  →  L = 28 cm

EX-06 (ITA-2007)

Um sistema massa-molas é constituído por molas de constantes k₁ e k₂, respectivamente, barras de massas desprezíveis e um corpo de massa m, como mostrado na figura. 

Solução:

Vamos aplicar o conceito de associação de molas:

a)      3 molas de K₂ em paralelo → 3K₂

b)      2 molas de K₁ em paralelo → 2K₁

Agora temos 3K₂ em série com 2K₁

Logo,

EX-07 (UFB)

Uma massa M=20/9kg, encontra-se suspensa ao conjunto de molas ilustrado na figura abaixo.  Suas constantes elásticas são k₁ = k₂=30N/m.

Calcule a constante elástica total equivalente do conjunto.

Solução:

Duas molas com K₂ estão em paralelo → K’₂ = 2.K₂ = 2.30 = 60 N/m

K’₂ está em série com K₁, então tem-se:

EX-08 (UNICAMP)

Nas cenas dos filmes e nas ilustrações gráficas do Homem-aranha, a espessura do cabo de teia de aranha que seria necessário para sustentá- lo é normalmente exagerada.

De fato, os fios de seda da teia de aranha são materiais extremamente resistentes e elásticos. Para deformações ΔL relativamente pequenas, um cabo feito de teia de aranha pode ser aproximado por uma mola de constante elástica k dada pela fórmula (K=10¹⁰ A/L), onde L é o comprimento inicial e A é a área da seção transversal do cabo. Para os cálculos abaixo, considere a massa do Homem-aranha M = 70 kg. Calcule a área A da seção transversal do cabo de teia de aranha que suportaria o peso do Homem-aranha com uma deformação de 1,0 % do comprimento inicial do cabo. (g=10m/s2).

Solução:

Dados: (Sistema Internacional – SI)

M = 70 kg

g = 10 m/s²

∆L = 1,0%L = 0,01L

K = 10¹⁰ A/L

Lei de Hooke:  P = F_elástico  → mg = K_*∆L → 70_*10 = 10¹⁰_*A/L_*0,01L →

700 = 10¹⁰_*A_*0,01 → A = 7x10^-6 → A = 7 μm²

EX-09

A intensidade da força elástica (F), em função das deformações (x) das molas A e B, são dadas pelo gráfico a seguir. Quando um corpo de peso 8 N é mantido em repouso, suspenso por essas molas, como ilustra a figura anexa; calcular a soma das deformações das molas A e B.

Solução:

Primeiramente, vamos calcular as constantes elásticas K_A e K_B das molas:

Do gráfico:

K_A = tgθ = F_A/x_A = 6/3 = 2 N/cm

K_B = tgθ’ = F_B/x_B =  4/5 = 0,8 N/cm

A constante elástica do sistema é:

K_eq = K_A*K_B/(K_A + K_B) = 2*0,8/(2+0,8) = 0,57 N/cm

O corpo está em equilíbrio, portanto,

P = F_mola  → m.g = Keq.∆y, onde Keq = constante elástica do sistema, ∆y = soma das deformações.

Logo,

8 = 0,57. ∆y  → ∆y ≈ 14,0351 cm  → ∆y = 14 cm  

EX-10

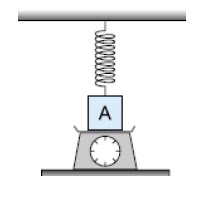
A mola da figura tem constante elástica 20 N/m e encontra-se alongada de 20 cm sob a ação do corpo A cujo peso é 5,0 N. Nessa situação de equilíbrio, determinar a indicação da balança, graduada em Newtons.

Solução:

Desenhando todas as forças que atuam no corpo A que está em equilíbrio, tem-se:

Onde

F_B = força de reação da balança (=indicação da balança);

F_M = força elástica da mola;

P = peso do corpo A

Dados:

K = 20 N/m

∆x = 20 cm = 0,20 m

P = 5 N

Portanto,

F_B + F_M = P → F_B = P – F_M  →  F_B = 5 – K.0,2 → F_B = 1 N