Fisica2015: Dinâmica - Exercícios Resolvidos

1) O carrinho da figura desliza no plano horizontal com aceleração 8 m/s². O corpo A possui 4 kg de massa e não há atrito entre o corpo e os planos de apoio. Dados sen30º=0,50 e cos30º=0,87. (g= 10 m/s²); determine a força horizontal que a parede vertical exerce sobre o corpo, considerando-o em repouso em relação ao carrinho.

Solução:

Vamos desenhar todas as forças sobre o corpo A:

E agora vamos decompor na direção dos eixos de referência:

Da figura-3 temos que:

Vamos tomar as equações (eq-1) e (eq-4) para calcular a N_R:

Agora temos todos os dados para calcular a força N_P (=força horizontal que vertical exerce sobre o corpo).

Nota: como os valores do seno e cosseno foram dados com 2 dígitos decimais, a reposta deve ser, também, em 2 dígitos decimais.

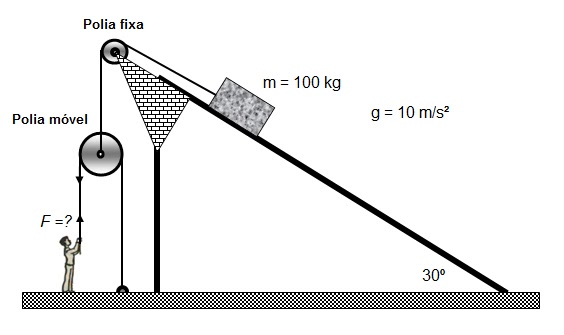
2) Determine o valor de F, (da figura), que o homem deve fazer para que o sistema fique em equilíbrio.

Solução:

Decompondo a força peso, temos que:

Como o sistema deve estar em equilíbrio:

T = P₁ = P.sen30º e

N = P₂=P.cos30º

Como devemos calcular a força F, estamos interessado na força de tração T.

E sabendo que sen30º=0,5, temos que:

T = 1000*0,5 = 500 N → T = 500 N

A polia fixa somente desvia (=somente altera) a direção da força e a polia móvel divide por dois a força que está aplicada ao seu eixo.

Portanto, F = T/2 = 500/2 = 250 N → F = 250 N

Resposta: O homem deve fazer uma força de 250 N para manter o equilíbrio do sistema.

3) As massas laterais de uma máquina de Atwood são de 400 g.

a) Que massa deve ser colocada num dos lados, a fim de que o conjunto adquira MRUA e percorra 1 m no primeiro segundo?

b) Tirando-se a sobrecarga depois de 1 s, que espaço percorre cada corpo lateral no segundo seguinte?

Adotar g = 10 m/s². Polia e fios são ideiais.

Solução:

Esquematicamente podemos representar uma máquina de Atwood como a figura a seguir:

a) m=? , MRUA (cinemática)

Portanto, a aceleração do sistema é igual a 2 m/s².

Para calcular a massa m vamos aplicar as equações da dinâmica:

b) Após 1 s, retira-se a sobrecarga, então temos MU.

Primeiramente vamos calcular a velocidade final do sistema em MRUA:

Portanto, quando se retira a sobrecarga o sistema continua em MU com velocidade v = 2 m/s², pois, não há qualquer tipo de atrito, ou força em oposição.

Logo, o espaço percorrido (pelo sistema) no segundo posterior à retirada da sobrecarga é:

∆s = v.t (v=2 m/s², t=1 s)

∆s = 2.1=2 m → ∆s = 2 m

Resposta: m=0,2 Kg e ∆s = 2 m

4) Um meteorito de 20 kg atravessa a atmosfera terrestre em 1 min e sua velocidade que era de 1000 m/s reduz-se para 400 m/s. Calcule a força oferecida pela atmosfera, considerando-a constante.

Solução:

Por hipótese:

a) m = massa constante

b) g = gravidade constante (10 m/s²)

c) α = desaceleração constante

Durante 60 s o movimento é MRUA, portanto:

Logo a desaceleração do meteorito durante os 60s foi de 10 m/s².

Como a α é, em módulo, igual a g = 10 m/s²; podemos afirmar que o meteorito chegou à velocidade limite, isto é, a velocidade será MU a partir deste momento em diante. Portanto, a força resultante F_R=P-R=0, logo P=R.

Então, temos que: R=m.(-10) = 20*(-10) = - 200 N → R = -200 N

(o sinal de “menos” é porque a força R se opõe ao movimento de queda, em outras palavras, foi adotado que o sentido da aceleração de gravidade como positivo (portanto, positivo para baixo)).

Resposta: A força de resistência da atmosfera é: - 200 N

5) Uma criança e seu pára-quedas têm a massa total de 70 kg. O diâmetro do círculo do pára-quedas é aproximadamente 6,5 metros. O coeficiente aerodinâmico do pára-quedas é da ordem K≈ 1,2 unidades SI. Determine a velocidade limite de queda. Considerar g=10 m/s².

Solução:

O sistema adquire velocidade limite v_Lquando R = P.

Com R = K.A.(v_L)² e P = m.g temos:

Onde m= 70 kg; g=10 m/s²; K=1,2 (SI) e A= 33 m² (=área da secção do pára-quedas de raio 6,5 m).

Portanto,

Resposta: A velocidade limite é, aproximadamente, 4,2 m/s.

6) Um bloco de peso igual a 600 N é puxado para cima, por meio de uma corda, paralela ao plano inclinado, como mostra a figura. Os atritos são desprezíveis e a corda é ideal. Adotar g=10 m/s². Determine:

a. a força F (em módulo) aplicada ao bloco para fazer subir com velocidade constante;

b. a força F (em módulo) que deve ser aplicada para que o bloco suba com aceleração constante de 1 m/s².

Solução:

a) Sobe com velocidade constante = Força resultante igual a zero = aceleração do bloco igual a zero.

Portanto,

F = P*sen30º= 600*1/2 = 300 N → F = 300 N

b) O bloco sobe com aceleração constante 1 m/s².

F_R = F – P*sen30º (1)

F_R = m*α (2)

(1) = (2) → F – P*sen30º = m*α → F = m*α + P*sen30º

Portanto,

F = 600/10*1+600*1/2 = 360 → F = 360 N

7) Sabendo-se que o sistema está em equilíbrio; calcular as trações nos fios, conforme a figura:

Solução:

De (eq.1) → P = T₁.sen30º → 1000 = T₁.0,5 → T₁ = 2000 N

e T₃ = P → T₃ = 1000 N

De (eq.2) → T₂ = T₁.cos30º

→ T₂ = 2000.√3/2 → T₂ = 1000.√3 N

Resposta: As forças de tração são: T₁ = 2000 N; T₂ = 1000.√3 N; T₃ = 1000 N

8) Sabendo-se que o sistema está em equilíbrio; calcular as trações nos fios, conforme a figura:

Solução:

Vamos aplicar aqui o Teorema de Lamy:

Sabendo-se que:

sen150^o = sen30^o = 1/2

sen120^o = sen60^o = √3/2

9) Qual o valor da força horizontal f, se a aceleração do conjunto é 1,5 m/s²? Desprezar os atritos e adotar g=10 m/s²

Solução:

O sistema não possui movimento vertical, pois todas as forças se anulam.

Na horizontal:

Resposta: a força horizontal é 9 N.

10) Uma esfera de 100 kgf apóia-se em dois planos inclinados, conforme indica o esquema. Sabe-se que, quando não há atrito, a força exercida por uma superfície em outra, nela encostada, é perpendicular às duas superfícies no ponto de contato. Calcule as reações nos pontos de contato.