Cinemática – Distância Mínima e Máxima

Distância mínima e máxima em relação à origem dos espaços do móvel cuja equação horária é do tipo função do 2º grau.

Genericamente temos: s(t) = c + bt + at²  e sabemos que as coordenadas do vértice no plano cartesiano são dadas por:  Vértice = (-b/2a, -∆/4a).  

Vamos deduzir as coordenadas do vértice: Vértice = (-b/2a, -∆/4a).  

Pelas figuras acima temos podemos afirmar que:

(1)     t₁ e t₂ são raízes da função horária;

(2)     t_v é ponto médio de t₁ e t₂.

Vamos tomar as raízes e substituir na equação: c + bt + at²  = 0

(t = t₁) →  c + bt₁+ at₁² = 0  (I)

(t = t₂) →  c + bt₂+ at₂² = 0  (II)

(I) = (II) → c + bt₁+ at₁² = c + bt₂+ at₂²  ↔  bt₁+ at₁² = bt₂+ at₂²  ↔

at₁² - at₂²  = bt₂ - bt₁  ↔  a(t₁² - t₂² ) = b(t₂ - t₁)  ↔ a( t₁ + t₂)(t₁ - t₂) = b(t₂ - t₁) = -b(t₁ – t₂)  ↔ a( t₁ + t₂) = -b  ↔ ( t₁ + t₂) = -b/a ↔  ( t₁ + t₂)/2 = -b/2a  (III)

Por outro lado: temos que t_v é ponto médio de t₁ e t₂, isto é:

t_v = ( t₁ + t₂)/2  (IV)

Comparando (III) e (IV) temos que:  t_v = -b/2a

Vamos calcular o Sv:

S(t_v=-b/2a) = c + b(-b/2a) + a(-b/2a)² = c –b²/2a + b²/4a = (4ac – b²)/4a = - (b²-4ac)/4a = -∆/4a  ↔  S_v = -∆/4a

Portanto, as coordenadas do vértice são: Vértice = (-b/2a, -∆/4a)

OUTRA MANEIRA DE OBTER RAPIDAMENTE AS COORDENADAS DO VÉRTICE É APLICAR O CONCEITO DE DERIVADA.

Seja uma equação horária genérica s(t) = c + bt + at².

A derivada ds(t)/dt = b+2at, para o ponto de mínimo, ou máximo, basta igualar a zero, então temos: 0 = b+2at ↔ t = -b/2a ↔ t_v = -b/2a

E para obter Sv, basta substituir na equação horária inicial e temos:

S(t_v=-b/2a) = c + b(-b/2a) + a(-b/2a)² = c –b²/2a + b²/4a = (4ac – b²)/4a = - (b²-4ac)/4a = -∆/4a  ↔  S_v = -∆/4a

Portanto, as coordenadas do vértice são: Vértice = (-b/2a, -∆/4a)

Cinemática - Gráficos do MU e MUV

Aplicações das funções matemáticas (constante, 1º grau e 2º grau) em cinemática.

1) Função constante

É a função y=k, onde k é um número real.  O gráfico da função constante é uma reta paralela ao eixo do x passando pelo ponto (x=0, y=k).  Figura-1.

Exemplos (em cinemática):

Quando um ponto material está em repouso (=parado) no quilômetro 100 de uma rodovia, seu espaço é constante com o tempo, figura-2; A velocidade v de um movimento uniforme é uma função constante com o tempo, figura-3; no movimento uniformemente acelerado MUV a aceleração é constante com o tempo, figura-4.

 2)  Função linear e função do 1º grau

Função linear é a função y=bx, onde b é um número real, diferente de zero. Seu gráfico é uma reta que passa pela origem O do plano cartesiano (Oxy), figura-5.

Função do 1º grau é a função y = bx + a, onde a e b são números reais (b≠0).  Seu gráfico também é uma reta, figura-6.  Se a=0, a função do 1º grau se reduz a uma função linear.

Exemplos (em cinemática):

A função horária do movimento uniforme (MU) s = s₀ + vt é do 1º grau em t, figura-7; e a função v = v₀ + αt da velocidade do MUV, também, é do 1º grau em t, figura-8.

3) Função do 2º grau

É a função y = a + bx + cx², onde a, b, c são números reais (c≠0).Seu gráfico é uma parábola.  Se o coeficiente c é positivo, a parábola tem concavidade voltada para cima, figura-09; se c é negativo, a concavidade é voltada para baixo, figura-10.

A função horária do movimento uniformemente variado (MUV) s = s₀ + v₀t + (α/2)t² é do tipo 2º grau em t.  O sinal da aceleração α determina a concavidade da parábola.  Se α > 0 é voltada para cima e se α < 0 é voltada para baixo, figura-11.

4) Coeficiente angular da reta

Na função do 1º grau y = a + bx, o número real b é chamado de coeficiente angular ou declive de reta representada no eixo cartesiano. O coeficiente angular b está associado ao ângulo θ da direção da reta com o eixo x, figura-12.

O coeficiente angular é numericamente igual à tangente trigonométrica do ângulo da direção da reta com o eixo x.

Se a função y = a + bx é crescente (figura-13), o coeficiente angular b é positivo e a tgθ é positiva. Se a função y = a + bx é descrescente (figura-14), o coeficiente angular é negativo e a tgθ é negativa.

A função horária s = f(t) do movimento uniforme é uma função do 1º grau em t, onde o coeficiente angular é a própria velocidade do movimento, 

figura-15:

A função da velocidade v = f(t) do movimento uniformemente variado (MUV) é uma função do 1º grau em t, onde o coeficiente angular é a própria aceleração do movimento, figura-16:

Vamos considerar o gráfico da função s = f(t) de um movimento qualquer, não uniforme (Fig-17).

Os tempos t₁ e t₂ correspondem às posições s₁ e s₂ (Fig-18).

A velocidade média neste intervalo de tempo é: 

Para determinar a velocidade instantânea em t₁ devemos calcular o valor limite de ∆s/∆t, quando ∆t → 0, ou t₂ → t₁ (como já foi visto na postagem anterior).

À medida que t₂ tende a t₁, o segmento P₁P₂ tende a tangente geométrica à curva do ponto P1 (Fig-19). 

Portanto, a velocidade instantânea em t₁ será medida pela tgθ, onde θ é o ângulo formado pela tangente geométrica à curva do ponto P₁ com o eixo t (Fig-20). 

Resumindo: se a função representada graficamente é a do 1º grau, o ângulo θ é o ângulo formado pela reta representativa da função com o eixo t (figura-21).

No entanto, se a função em estudo não é do 1º grau, o ângulo θ será o ângulo formado pela tangente geométrica à curva com o eixo t (Fig-22).

De forma análoga, podemos aplicar os mesmos procedimentos para a função velocidade v = f(t); sendo que neste caso, a tgθ nos fornece a aceleração α do movimento (Fig-23).

Todas as propriedades gráficas anteriores podem ser resumidas em EVA, sendo E indica o espaço, V a velocidade e A igual à aceleração:

Em outras palavras: no gráfico do espaço em função do tempo, a tgθ nos fornece a velocidade; no gráfico da velocidade em função do tempo, a tgθ nos fornece a aceleração.

5)  Cálculos de áreas em cinemática.

No movimento uniforme (MU) a velocidade é uma função constante com o tempo (Fig-24).  Nessa figura,  o número que mede a área A é igual ao número que mede o espaço percorrido ∆s no intervalo de tempo t₁ e t₂.

Verifiquemos essa propriedade considerando o movimento:

s = 5 + 10t (t→s, s→m), onde v=10 m/s=constante.

A = 2 x 10 = 20; portanto a área é numericamente igual ao espaço percorrido nesse intervalo de tempo.

Essa propriedade é verdadeira para qualquer tipo de movimento. Na figura-25, no gráfico da velocidade em função do tempo, a área A da região, delimitada pela curva e o eixo das abscissas é numericamente igual ao espaço percorrido (∆s) pelo móvel nesse intervalo de tempo.

No movimento uniformemente variado (MUV) cuja velocidade varia com o tempo, segundo a equação:

v = 10 + 2t  (t→s, v→m/s) e α = 2 m/s²

No gráfico da aceleração α em função do tempo (Fig-26), a área A é numericamente igual à variação de velocidade ∆v, no intervalo de tempo de t₁ = 2s  e  t₂ = 4s.

No gráfico-26, a área A é A = 2 x 2 = 4, portanto, ∆v = 4 m/s

Essa propriedade é válida em qualquer tipo de movimento.  A aceleração em função do tempo, na figura-27, a área A da região delimitada pela curva e o eixo das abscissas é numericamente igual à variação de velocidade (∆v) do móvel nesse intervalo de tempo.

As propriedades gráficas estudadas neste item resultam em AVE.  Onde A=aceleração, V=velocidade e E=espaço.

Assim, no gráfico da aceleração em função do tempo, numericamente a área A mede a variação de velocidade.  No gráfico da velocidade em função do tempo, numericamente a área A mede o espaço percorrido.

6) Juntando EVA e AVE, temos:

Nota-se que fundamentalmente, há 2 tipos de cálculos em gráficos:

O cálculo da tgθ; tangente trigonométrica do ângulo da inclinação da reta, que tangencia geometricamente, em um ponto, o gráfico da função(Fig28).

O cálculo da área A da região delimitada pelo gráfico da função, e pelo eixo dos tempos e pelos 2 segmentos de reta perpendiculares ao eixo dos tempos (Fig-29). 

Cinemática - Ex.Resolvidos-02-SOLUÇÕES

R01)

A velocidade do floco de algodão quando chega ao chão.

v = v₀ + g.t →  v = 0 + 10*6 = 60 m/s →  v = 60 m/s

Logo, devemos lançar um pedaço de ferro, de baixo para cima, com velocidade de 60 m/s, para que o pedaço de ferro   atinja a mesma altura de onde o floco de algodão iniciou a queda.

E a equação que descreve a velocidade é: v = 60 – 10.t

R02)

s = s₀ + v₀t –gt²/2 = 0 + 147t – 4,9t² → s = 147t – 4,9t² (equação horária)

v = v₀ – gt = 147 – 9,8t  →  v = 147 – 9,8t  (equação da velocidade)

R03)

A equação horária do movimento é: h = h₀ + v₀t + gt²/2  (h→m, t→s)

Adotando a origem dos espaços onde o corpo é lançado: h₀ = 0

Então, h = 50.t  + 5.t² = 50*12 + 5*12² = 12*50 + 5*12*12 = 12*(50+60) = 12*110 = 1320 → h = 1320m

R04)

Para calcular o tempo que o corpo leva do ponto A até parada total, pode ser descrito pela seguinte equação: v = v_A + α*t, v = 0  → 0 = 60 + α*t (I)

Para obter o valor (α) de desaceleração, vamos aplicar a equação de Torricelli, entre os pontos A e B.

(II) v² = v₀² + 2α∆s, v=50, v₀=60, ∆s=275, α=?  (v→m/s, s→m, α→m/s²)

50² = 60² + 2*α*275 → 50² - 60² = 2*α*275 → (50+60)*(50-60) = 2*α*275 →

110*(-10) = 2*α*275 → 110* (-5) = α*275 → - 110 = α*55 → α = - 2m/s²     

( I )  0 = 60 + α*t  ↔ 0 = 60 -2*t  ↔  t = 30 s

R05)

A equação horária para MUV:

s = s₀ + v₀*t + α*t²/2

s₀ = 60 m

v₀ = 5 m/s

α = 4 m/s²

Logo, s = 60 +5*t + 2*t²

R06)

Sabemos que:

Dados:

t₁ = 30 s, v₁ = 72 km/h = 20 m/s

t₂ = 110 s, v₂ = 144 km/h = 40 m/s

α_m  = (40 – 20)/(110 – 30) = 20/80 = 0,25  → α_m  = 0,25 m/s²

R07)

Aceleração instantânea em t=4s,  v = 5 + 2.t², ( v → m/s, t → s)

Vamos tomar um tempo (t - ∆t), onde ∆t é intervalo de tempo pequeno antes de 4 segundos.

v₁ = v ( t- ∆t) = 5 + 2*(t - ∆t)² = 5 + 2*(t² - 2*t*∆t +∆t²) = 5 + 2*t² - 4*t*∆t +2*∆t²

e

v₂ = v (t) = 5 + 2*t²

∆v/∆t = v₂ - v₁ / ∆t = (5 + 2*t²) – (5 + 2*t² - 4*t*∆t +2*∆t²) / t – (t - ∆t) =

= (4*t*∆t - 2*∆t²)/∆t = 4*t – 2*∆t

lim   (4*t – 2*∆t)   =  4*t, (∆t→0, então, t = 4 s) → α = 4*t = 4*4 =16

∆t →0                                                                        

Logo, a aceleração instantânea em t=4s é igual a α = 16 m/s²

R08)

Trata-se de movimento uniforme (MU).

(1)  s₁=v₁*t₁ → d = 80* t₁  → t₁ = d/80

(2)  s₂=v₂*t₂ → d = 60* t₂  → t₂ = d/60

Velocidade média em todo o percurso:

V_m = ∆S/∆T  →  V_m = (d + d)/(t₁ + t₂) = 2d/[d/80+d/60] = 2d*(60*80)/d(60+80) = 68,57.

V_m = 68,57 km/h

Notar que a velocidade média no percurso total não é a média aritmética das duas velocidades.

R09)

A) Os dois navios partem ao mesmo tempo e movem-se no mesmo sentido.

Como os 2 navios partem do mesmo ponto; para que haja uma distância de 600 km entre eles é a mesma coisa que um navio com a velocidade (35 – 25) km/h, percorrendo os 600 km.

∆s = v*∆t → ∆t = ∆s/v = 600/10 = 60 h → ∆t = 60 h

B) O navio mais lento parte 2 horas antes do outro e movem-se no mesmo sentido;

Como o navio mais lento partiu 2 horas antes do navio mais rápido.

Temos que: Em 2 horas o navio mais lento percorreu uma distância de: ∆s = v*∆t = 25*2 = 50 km.

Portanto, o navio mais rápido deve percorrer os 50 km (para alcançar) o navio mais lento e depois tem ainda 600 km para não perder a comunicação.  Então, podemos substituir por um navio de velocidade (35-25) = 10 km/h, percorrendo os (50 +600) = 650 km.

Logo:   ∆s = v*∆t → ∆t = ∆s/v = 650/10 = 65 h → ∆t = 65 h

C) Os dois navios partem ao mesmo tempo e movem-se em sentidos opostos.

Os navios se movem em sentidos opostos, então, a velocidade relativa é soma das velocidades: (35 + 25) = 60 km/h.

Podemos substituir por um navio de velocidade 60 km/h, percorrendo 600 km.

Logo:   ∆s = v*∆t → ∆t = ∆s/v = 600/60 = 10 h → ∆t = 10 h

R10)

A) Trens no mesmo sentido:

∆s = v*∆t → ∆t = ∆s/v = 0,50/20 = 0,025 h → ∆t = 0,025 h

B) Trens em sentidos contrários:

∆s = v*∆t → ∆t = ∆s/v = 0,50/100 = 0,005 h → ∆t = 0,005 h

R11)

∆s = v*∆t → ∆t = ∆s/v = 0,100/40 = 0,0025 h → ∆t = 0,0025 h

R12)

Quando o automóvel ultrapassa o trem a posição do trem e do automóvel são iguais e o tempo gasto também são iguais.  Portanto,

s_trem = (s₀)_trem + v_trem*t   (1)

s_auto = v_auto*t = 2* v_trem*t  (2)

Comparando as equações (1) e (2)

strem = sauto  ↔  (s₀)_trem + v_trem*t = 2* v_trem*t  ↔  100 + v_trem*t = 2* v_trem*t  ↔ v_trem*t = 100

De equação (2)

s_auto = v_auto*t = 2* v_trem*t  → s_auto = 2* v_trem*t  = 2*100  → s_auto = 200

Como adotamos como a origem dos espaços, quando o automóvel inicia a ultrapassagem:

∆s_auto  = 200 m

R13)

Dados:

v = 12 – 3t, onde v (m/s) e t (s).

s₀ = 4 m

Pede-se: s (t=10 s) = ?

Trata-se de MUV:  logo v = v₀ +αt,

Então por comparação temos: v₀ = 12 m/s e α = ─3 m/s²

A equação horária é: s = s₀ + v₀t + αt²/2

Então: s = 4 +12t -3t²/2  → (t=10s) →  s= 4 +12*10 – 3*10*10/2 = ─ 26 m  →

s = ─ 26 m  

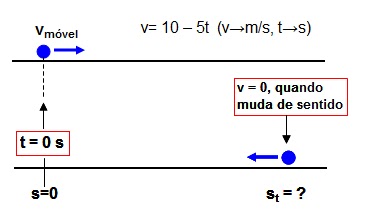
R14)

Dados:

v= 10 – 5t  (v→m/s, t→s)

Pede-se: a posição do móvel, quando mudar de sentido.

Quando muda de sentido: v = 0

Logo: 0 = 10 – 5t  ↔  t = 2 s

Vamos determinar a equação horária do móvel: 

Temos que da equação da velocidade dada: v_o = 10 m/s e α = ─ 5 m/s²

E a posição inicial:  s₀ = 0

MUV:  s = s₀ + v₀t + αt²/2

Logo:  s = 0 + 10t  - 5t²/2

Então, t = 2 → s = 10*2 -5*2²/2 = 10*2 – 10*1 = 10 → s = 10 m

R15)

MUV:  s = s₀ + v₀t + αt²/2  e v = v₀ + αt

Como está freando: s = s₀ + v₀t - αt²/2  e v = v₀ - αt

Vamos calcular a velocidade inicial:

v = v₀ – αt ↔ 0 = v₀ – 10*5 ↔ v₀ = 50 m/s

Agora, vamos calcular a distância que percorreu durante a frenagem:

s = s₀ + v₀t - αt²/2  ↔ ∆s = v₀t - αt²/2  = 50*5 – 10*5²/2 = 125 m ↔ ∆s = 125 m

R16)

Vamos considerar que no espaço entre o posto terrestre e o navio as velocidades do som no ar e na água são constantes.  Portanto, MU.

Como        (V_SOM)_ÁGUA   > (V_SOM)_AR   →  t_AR = t_ÁGUA + 5  (t = tempo em segundos)

No ar:

∆s = v* t_AR = 341* t_AR   (1)

N água:

∆s = v* t_ÁGUA = 1.504* t_ÁGUA   = 1.504*(t_AR – 5)   (2)

Igualando as equações (1) e (2), temos:

341* t_AR   = 1.504*(t_AR – 5)   →  341* t_AR   = 1.504*t_AR  - 5*1.504  ↔  t_AR  ≈ 6,47 s

Portanto, para calcular o valor de “x”, podemos tomar a equação (1):

(1)   ∆s = v* t_AR = 341* t_AR   = 341*6,47 ≈ 2.206 m   →  x = 2.206 m

R17)
Movimentos uniformes (MU)

Até o ponto de cruzamento:

TR1:    d1 = V1*∆t1

TR2:    d2 = V2*∆t2

No cruzamento:  ∆t1 = ∆t2 →  d1/V1 = d2/V2  →  d2/d1 = V2/V1  (1)

Após o cruzamento:

TR1:   d2 = V1*25

TR2:   d1 = V2*49

Logo,  d2/d1 = V1*25/V2*49 (2)

Portanto:

Fazendo (1) = (2)  → V2/V1 = V1*25/V2*49  →  (V1)²/(V2)² = 49/25 = 7²/5²  ↔ V1/V2 = 7/5

R18)

Na frenagem:

V₀ = 90 km/h = 25 m/s

V= 18 km/h = 5 m/s

Logo o tempo gasto foi:  ∆V = - αt → t = ∆V/-α  →  t = (5 – 25)/- 0,40 = 50 s  → t=50 s

Vamos calcular a distância que percorreu durante a frenagem:

∆S = V₀ *t – αt²/2 = 25*50 – 0,4*50²/2 = 750 m

O tempo que gastaria com velocidade 25 m/s (MU):

∆t = ∆S/V = 750/25 = 30 s

Portanto, a perda de tempo foi de:  50 – 30 = 20 s

No deslocamento na obra (600 m):

1)     Se percorresse com velocidade de 25 m/s (90 kmh):  ∆t = ∆S/V = 600/25 = 24 s  →  ∆t = 24 s

2)     Percorreu com a velocidade de 5 m/s (18 km/h):  ∆t = ∆S/V = 600/5 = 120 s  → ∆t = 120 s

Logo, o tempo de atraso é: 120 – 24 = 96 s

Na aceleração de retomada de velocidade:

V₀ = 18 km/h = 5 m/s

V= 90 km/h = 25 m/s

Portanto o tempo gasto foi: ∆V =  αt → t = ∆V/α  →  t = (25 – 5)/ 0,20 = 100 s → t = 100 s

Calculando a distância percorrida durante a aceleração:

 ∆S = V₀ *t + αt²/2 = 5*100 + 0,2*100²/2 = 500 + 1000 = 1.500 →  ∆S = 1.500 m

O tempo que gastaria com velocidade 25 m/s (MU):

∆t = ∆S/V = 1.500/25 = 60 s

Logo, o tempo de atraso é:  100 – 60 = 40 s

Logo o tempo total de atraso é:  20 + 96 + 40 = 156 s

R19)

MUV

V = V₀ + αt

V² = (V₀)² + 2α∆S (equação de Torricelli)

No trecho AB, temos que:

V₀ = 36 km/h = 10 m/s

V = 54 km/h = 15 m/s

∆S = 100 m

Aplicando Torricelli para calcular a aceleração:

V² = (V₀)² + 2α∆S  →  15² = 10² + 2*α*100  →  α = 0,625 m/s²

Agora, da equação da velocidade podemos calcular o tempo gasto:

V = V₀ + α∆t  →  15 = 10 + 0,625*∆t  →   ∆t = 5/0,625 = 8 s  →  ∆t = 8 s

Calcular a distância ∆S decorridos (t = 8 + 10 = 18 s), partindo do ponto A.

De equação horária:

V₀ = 10 m/s

α = 0,625 m/s²

t = 18 s

S = S₀ + V₀t + αt²/2  →  ∆S =  10*18 + 0,625*18²/2 = 180 + 101,25 = 281,25 m

Portanto, ∆S =  281,25 m

Velocidade neste instante é:

V = V₀ + αt  →  V = 10 + 0,625*18 = 21,25 m/s  →  V =  21,25 m/s  

R20)

MRUV:

V = V₀ + αt

S = S₀ + V₀t + αt²/2

Temos que:

(1)     ─ 4 = V₀ + α*2    →  ─ 4 = V₀ + 2α

(2)     ─ W = V₀ + α*5   → ─ W = V₀ + 5α 

(3)      W = V₀ + α*7  →  W = V₀ + 7α

Tomando as equações (2) e (3):

Agora pegando as equações (1) e (4):

Substituindo em (1):

Sabemos que S=4,5 m para t=3s, então temos que:

S = S₀ + V₀t + αt²/2

4,5 = S₀ ─ 6*3 +1*(3)²/2 = S₀ ─ 18 + 4,5  →  4,5 = S₀ ─ 18 + 4,5  → S₀ = 18 m/s

Portanto, a equação horária [ s = f(t)] do ponto material é:

S = S₀ + V₀t + αt²/2   →  S = 18 ─ 6t + t²/2