Força de Atrito - Ex.Resolvidos-1

EX-01 – Física Kazuhito/Fuke – Pág.242 – EP5

Um bloco de acrílico de 0,5 kg é puxado por fio com uma força de 7 N. A direção da força é paralela à superfície horizontal da mesa onde está apoiado o bloco, que adquire a aceleração de 2 m/s². Essa aceleração só pode ser explicada se houver a ação de uma força de atrito de que intensidade?

Solução:

Aplicando a Equação Fundamental da Dinâmica, tem-se:

F – F_at = m.a  → 7 - F_at = 0,5_*2  → – F_at = 1 – 7 → F_at = 6 N

EX-02– Física Kazuhito/Fuke – Pág.243 – EP6

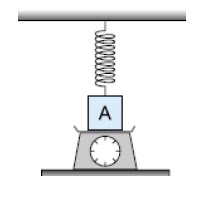
O esquema experimental, mostrado abaixo, é composto de dois blocos: A e B. Suas massas são, respectivamente, iguais a 10 kg e 11 kg.

São dados, com arredondamento: sen37º = 0,6 e cos37º = 0,8.

Se o bloco A estiver subindo com velocidade constante, onde g = 10 m/s², determine:

a)    O módulo da tração no fio ideal;

b)    A intensidade da força de atrito entre o bloco A e o plano inclinado;

c)    O coeficiente de atrito do item anterior.

Solução:

Desenhando todas as forças envolvidas no sistema:

Pelo enunciado, temos:

1)      O sistema de movimento com velocidade constante → aceleração do sistema é zero (a = 0).

2)      sen37º = 0,6 e cos37º = 0,8.

3)      mA = 10 kg e mB = 11 kg

4)      g = 10 m/s²

a)    Calculando o Módulo da Tração:

 Bloco B

 T = P_B = m_B*g = 11*10 = 110 N →  T = 110 N

b)    Calculando a Força de Atrito:

Bloco A

PA = m_A*g = 10*10 = 100 N

T = P_A*sen37º + F_at → F_at = T - P_A*sen37º = 110 – 100*0,6 = 50 N → F_at = 50 N

c)    Calculando o coeficiente de atrito:

Fat = μ*N → 50 = μ*100*0,8 → μ = 50/80 = 0,625 →

μ = 0,625

EX-03– Física Kazuhito/Fuke – Pág.243 – EP10

Uma xícara de 0,4 kg está sobre uma mesa horizontal. O coeficiente de atrito entre eles é 0,20 para o estático e 0,15 para o dinâmico.  Então, ao aplicamos uma força horizontal de intensidade igual a 0,5 N, qual é o módulo da força de atrito que surge na xícara? Dado: g = 10 m/s².

Solução:

P = m.g = 0,4*10 = 4 N, portanto, força normal é igual a 4 N, logo:

Calculando a força de atrito estático:

(F_at)_e = μ_e*N = 0,20*4 = 0,8 N  → (F_at)_e = 0,8 N 

Como a força F é menor que força de atrito estático, portanto, a xícara não se movimenta.

Logo, a força de atrito é igual à força F aplicada, porque está em repouso.

(F_at) = 5 N

EX-04– Física Kazuhito/Fuke – Pág.243 – EP11

Qual seria a aceleração do movimento da xícara, no exercício anterior, se a força motriz tivesse 1 N de intensidade?

Solução:

Do exercício anterior:

(F_at)_e = 0,8 N 

Como agora a força F (motriz) é 1 N, portanto, maior, logo, a xícara se move.

Durante o movimento temos a força de atrito dinâmica:

(F_at)_d = 0,15*4 = 0,6 N  → (F_at)_d = 0,6 N

Vamos calcular a aceleração da xícara, aplicando a Equação Fundamental da Dinâmica:

F_R = m*a ↔ F – (F_at)_d  = 0,4*a  ↔ 1 – 0,6 = 0,4*a ↔ 0,4 = 0,4*a ↔ a = 1 m/s²

EX-05– Física Kazuhito/Fuke – Pág.243 – EP12

Uma caixa de papel, de massa 5 kg, está em repouso sobre uma superfície plana e horizontal. O diagrama mostra a variação da força de atrito sobre a caixa quando nela atua uma força de módulo F variável, paralela à superfície. Dado: g=10 m/s².

a) Calcule os coeficientes de atrito estático e dinâmico;

b) Qual é a aceleração adquirida pela caixa quando F = 20 N?

Solução:

a)

Na iminência de movimento (de gráfico):

(F_at)_e = μ_e*N  → 15 = μ_e*5_*10  → μ_e = 0,3

Em movimento (de gráfico):

(F_at)_d = μ_d*N  → 10 = μ_d*5_*10  → μ_d = 0,2

b)

Aplicação da Equação Fundamental da Dinâmica:

F – F_at = m.a  →  a = (F – F_at)/m = (20 – 0,2*50)/5 = 2  → a = 2 m/s²

EX-06– Física Kazuhito/Fuke – Pág.244 – EP16 (UNIFESP)

Conforme noticiou um site da Internet em 30.8.2006, cientistas da Universidade de Berkeley, Estados Unidos, “criaram uma malha de microfibras sintéticas que utilizam um efeito de altíssima fricção para sustentar cargas em superfícies lisas”, à semelhança dos “incríveis pelos das patas das lagartixas”. (www.inovacaotecnologica.com.br). 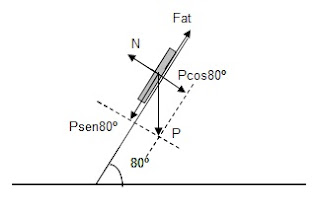Segundo esse site, os pesquisadores demonstraram que a malha criada “consegue suportar uma moeda sobre uma superfície de vidro inclinada a até 80º” (veja a foto).

Dados sen 80º = 0,98; cos 80º = 0,17 e tg 80º = 5,7, pode-se afirmar que, nessa situação, o módulo da força de atrito estático máxima entre essa malha, que reveste a face de apoio da moeda, e o vidro, em relação ao módulo do peso da moeda, equivale a, aproximadamente de:

Solução:

Na iminência de movimento: (F_at)_e = P.sen80º

EX-07 (UNICAMP)

Um caminhão transporta um bloco de ferro de 3,0t, trafegando horizontalmente e em linha reta, com velocidade constante. O motorista vê o sinal (semáforo) ficar vermelho e aciona os freios, aplicando uma desaceleração constante de valor 3,0 m/s2. O bloco não escorrega. O coeficiente de atrito estático entre o bloco e a carroceria é 0,40. Adote g = 10 m/s2.

a) Qual a intensidade da força de atrito que a carroceria aplica sobre o bloco, durante a desaceleração?

b) Qual é a máxima desaceleração que o caminhão pode ter para o bloco não escorregar?

Solução:

a)

O bloco não escorrega:

Então o módulo da força de atrito é igual a força motriz, logo:

Fat = F = m*a ↔ Fat = 3000*3 = 9 000 N ↔ Fat = 9 kN

b)

a_máx = ?

A desaceleração máxima permissível acontece na iminência do bloco de ferro se mover.

Portanto:

(Fat)e = m*a_máx ↔  μe*N = m*a_máx ↔  μe*N = 3000* a_máx ↔ 0,4*3000*10 = 3000* a_máx ↔ a_máx = 4 m/s²

EX-08 (UFV)

Uma corda de massa desprezível pode suportar uma força tensora máxima de 200N sem se romper. Um garoto puxa, por meio desta corda esticada horizontalmente, uma caixa de 500N de peso ao longo de piso horizontal. Sabendo que o coeficiente de atrito cinético entre a caixa e o piso é 0,20 e, além disso, considerando a aceleração da gravidade igual a 10 m/s2, determine:

a) a massa da caixa;

b) a intensidade da força de atrito cinético entre a caixa e o piso;

c) a máxima aceleração que se pode imprimir à caixa.

Solução:

a)

P = 500 → m*g = 500 → m*10 = 500 → m = 50 kg

b)

(Fat)_d = μ_d*N  → (Fat)_d = 0,2*500 = 100 → (Fat)_d = 100 N

c)

Máxima aceleração = iminência de movimento

100 = 50*a → a = 2 m/s²

EX-09 (AMAN)

Um bloco de 1,0kg está sobre outro de 4,0kg que repousa sobre uma mesa lisa. Os coeficientes de atrito estático e cinemático entre os blocos valem 0,60 e 0,40. A força F aplicada ao bloco de 4,0kg é de 25N e a aceleração da gravidade no local é aproximadamente igual a 10 m/s². Qual é a intensidade da força de atrito que atua sobre o bloco de 4,0kg?

Solução:

Vamos calcular a aceleração do sistema:

A força resultante é 25 N, portanto,

F_R = m.a → 25 = 5.a → a = 5 m/s²

Bloco A:

(Fat)_e = μ_e*N = 0,6*10 = 6 → (Fat)_e = 6 N

Força motriz:

F = m.a → F = 1*5 = 5 → F = 5 N

Como força motriz é inferior a força de atrito estático, o bloco A não se move em relação ao bloco B.

Logo, força de atrito que atua sobre o bloco B é: Fat = 5 N

EX-10 (PUC MG)

No sistema mecânico da figura, os corpos A e B têm massas m_A = 6,0 kg e m_B = 4,0 kg, respectivamente. O fio que os une e a polia são ideais. O coeficiente de atrito entre o plano horizontal e o corpo A é m. A resistência do ar é desprezível e, no local, a aceleração da gravidade é g = 10m/s². Quando o sistema é abandonado do repouso da posição indicada na figura, a aceleração por ele adquirida tem módulo de 1,0 m/s².

Calcule:

a) a intensidade da força que traciona o fio;

b) o valor de m.

Solução:

Bloco B:

F_R = P_B – T

P_B – T = m_B*a → 40 – T = 4*1 → T = 36 N

Bloco A:

T – Fat = m_A*a  → T – μ*N = m_A*a →  36 – μ*60 = 6*1 → μ = 0,5

Força de Atrito

A força de atrito é uma força que faz resistência ao movimento do corpo e atua sempre em paralelo ao movimento e esta força surge devido à rugosidade das superfícies que estão em contato. E é uma força proporcional à força Normal.

Resumindo:

• Opõe-se ao movimento;
• Depende da rugosidade e a natureza das superfícies (coeficiente de rugosidade)
• É proporcional à força Normal;
• Transforma a energia cinética em energia calorífica (dissipada ao meio ambiente).

A força de atrito é calculada pela seguinte equação:

Onde:

μ: coeficiente de atrito (adimensional)

N: Força normal (N)

Temos duas situações:

Força de atrito estático: quando o corpo estiver sem deslizamento (em repouso);

A força de atrito estático máxima é igual à força mínima necessária para iniciar o movimento de um corpo.

Quando um corpo não está em movimento, a força de atrito deve ser maior que a força aplicada; neste caso, é usado no cálculo um coeficiente de atrito estático: μ_e

Então:

Força de atrito dinâmico: quando o corpo está em movimento.

Aplica-se uma força (empurrando, ou puxando) sobre o corpo para que este entre em movimento; para que o corpo entre em movimento a força aplicada deve ser superior à força de atrito estático.

Quando a força de atrito estático for ultrapassada pela força aplicada ao corpo, este entrará em movimento, e passaremos a considerar sua força de atrito dinâmico.

A força de atrito dinâmico é sempre menor que a força aplicada; no seu cálculo é utilizado o coeficiente de atrito cinético: μ_d

Então:

Método empírico para a determinação do coeficiente de atrito estático.

Da noção de iminência de movimento podemos estabelecer um método experimental simples para a determinação do coeficiente de atrito estático. Inclinamos aos poucos o plano de apoio até o instante em que o corpo fique na iminência de escorregar. Quando o corpo está na iminência de escorregar, a força de atrito atinge seu valor máximo:

Estando o corpo em equilíbrio, decorre que (F_at)_max  e  P_*senθ devem ser iguais:

Então, temos que:

(F_at)_max = P_*senθ ↔ μ_e*P_*cosθ = P_*senθ ↔ μ_e = senθ/cosθ ↔ μ_e = tgθ

Aumentando gradativamente o ângulo θ e colocar o corpo na iminência de escorregar e medir o ângulo θ.

O valor da tangente do ângulo θ é o coeficiente de atrito estático: μ_e = tgθ

Resumindo temos:

1)    Corpo em repouso:  0 ≤ F_at ≤ μ_e*N

2)    Corpo em movimento: F_at = μ_d*N

Força de atrito viscoso: quando um corpo se movimenta no fluido (água ou ar), sofre a ação de uma força de resistência, portanto, no sentido contrário ao do movimento.  Encontramos outras duas denominações: força de atrito fluido e força de resistência do fluido.

Tem-se fórmula empírica (=experimental):

Onde:

v = módulo da velocidade do corpo em relação ao fluido.

n = constante que depende da ordem de grandeza da velocidade e do tamanho do corpo, geralmente temos n = 1 ou n = 2.

k = constante que depende da natureza do fluido (bem como de sua temperatura e densidade), do formato do corpo e da área da maior seção reta do corpo, perpendicular à direção do movimento (quanto maior essa área, maior o valor de k).

Força de empuxo: quando um está dentro de um fluido, além da força de atrito viscoso (que só existe quando o corpo está em movimento em relação ao fluido), o fluido aplica ao corpo outra força (que existe mesmo quando o corpo está parado) chamada de Empuxo (E).

O Empuxo tem sentido oposto ao da aceleração da gravidade e o módulo é dado por:

Onde:

g = módulo da aceleração da gravidade;

V = volume do corpo;

d = densidade do fluido

Força Elástica Exercícios Resolvidos-1

EX-01 (UFRJ - 2007)

Um bloco de massa 5 kg está parado sobre um plano inclinado de um ângulo de 30° com a horizontal, preso a uma mola, de constante elástica k = 100 N/m, como mostra a figura. O atrito entre o bloco e o plano pode ser desprezado.

a) Represente as forças que atuam na caixa e escreva quem exerce cada uma das forças.

b) Calcule a deformação da mola nessa situação.

Solução:

Calculando a deformação x da mola:

Dados: m = 5 kg; k = 100 N/m

Adotar: g = 10 m/s²

Se F_M = Psen30º → k.x = m.g.1/2 → 100.x = 5.10.1/2 → x = 0,25 m →

x = 25 cm

EX-02 (UFB)

Entre dois blocos 1 e 2 de massas m₁=12 kg e m₂=8 kg existe uma mola ideal A. Os dois blocos estão apoiados sobre

um plano horizontal sem atrito. O bloco 1 é puxado por uma força F constante, horizontal e paralela ao plano por meio de outra mola ideal B, idêntica à mola A. Calcule a relação x_A/x_B entre as deformações das molas A e B, depois que o sistema entrou em movimento com aceleração constante a.

Solução:

EX-03 (UFPE 2005)

Duas molas A e B de comprimentos iguais a L, mas de constantes elásticas diferentes ( K_A = 0,2 K_B ), são unidas no ponto C e alongadas até o comprimento total 4L. Os terminais das molas são então fixados em suportes rígidos, como mostra a figura. Determine a razão, L_A/L_B entre os comprimentos das molas nessa situação

Solução:

Dados:

K_A = 0,2 K_B

L_A + L_B = 4L

Temos que:

L_A = L + x_A  (sendo x_A  é a deformação da mola A)

L_B = L + x_B  (sendo x_B  é a deformação da mola B)

E como o ponto C está em equilíbrio, tem-se:

K_A.x_A = K_B.x_B  →  0,2K_B.x_A=K_B.x_B  →  x_A = 5.x_B  (1)

L_A + L_B = 4L →  (L + x_A) + (L + x_B) = 4L →  2L + x_A + x_B = 4L →

x_A + x_B = 2L (2)

(1) em (2) → 5.x_B  + x_B = 2L →  6.x_B = 2L  →  x_B = 1.L/3

Logo, x_A = 5.x_B  → x_A = 5L/3

Portanto,

EX-04 (UFSM)

Durante os exercícios de força realizados por um corredor, é usada uma tira de borracha presa ao seu abdome. Nos arranques, o atleta obtém os seguintes resultados:

O máximo de força atingido pelo atleta, sabendo-se que a constante elástica da tira é de 300 N/m e que obedece à lei de Hooke, é, em N,

a) 23520       b) 17600        c) 1760       d) 840        e) 84

Solução:

Lei de Hooke:  F_elástico = K.∆x, portanto, a força é máxima para ∆x máximo.

Logo,

F_max = K.∆x → F_max = 300.0,28 = 84 →  F_max = 84 N

Resposta: alternativa e

EX-05 (Mackenzie-SP)

A mola da figura varia seu comprimento de 10cm para 22cm quando penduramos em sua extremidade um corpo de 4N. 

Determine o comprimento total dessa mola quando penduramos nela um corpo de 6N.

Solução:

A deformação da mola para carga de 4 N foi de ∆x = 22 – 10 = 12 cm.

Logo, podemos calcular a constante de mola K:

F=K.∆x → 4 = K.0,12 → K = 100/3 N/m

Portanto, a deformação para uma carga de 6 N será:

F’=K.∆x’ → 6 = 100/3. ∆x’ → ∆x’ = 0,18 m  →  ∆x’ = 18 cm 

Logo, o comprimento total da mola é:

L = 10 + 18 = 28 cm  →  L = 28 cm

EX-06 (ITA-2007)

Um sistema massa-molas é constituído por molas de constantes k₁ e k₂, respectivamente, barras de massas desprezíveis e um corpo de massa m, como mostrado na figura. 

Solução:

Vamos aplicar o conceito de associação de molas:

a)      3 molas de K₂ em paralelo → 3K₂

b)      2 molas de K₁ em paralelo → 2K₁

Agora temos 3K₂ em série com 2K₁

Logo,

EX-07 (UFB)

Uma massa M=20/9kg, encontra-se suspensa ao conjunto de molas ilustrado na figura abaixo.  Suas constantes elásticas são k₁ = k₂=30N/m.

Calcule a constante elástica total equivalente do conjunto.

Solução:

Duas molas com K₂ estão em paralelo → K’₂ = 2.K₂ = 2.30 = 60 N/m

K’₂ está em série com K₁, então tem-se:

EX-08 (UNICAMP)

Nas cenas dos filmes e nas ilustrações gráficas do Homem-aranha, a espessura do cabo de teia de aranha que seria necessário para sustentá- lo é normalmente exagerada.

De fato, os fios de seda da teia de aranha são materiais extremamente resistentes e elásticos. Para deformações ΔL relativamente pequenas, um cabo feito de teia de aranha pode ser aproximado por uma mola de constante elástica k dada pela fórmula (K=10¹⁰ A/L), onde L é o comprimento inicial e A é a área da seção transversal do cabo. Para os cálculos abaixo, considere a massa do Homem-aranha M = 70 kg. Calcule a área A da seção transversal do cabo de teia de aranha que suportaria o peso do Homem-aranha com uma deformação de 1,0 % do comprimento inicial do cabo. (g=10m/s2).

Solução:

Dados: (Sistema Internacional – SI)

M = 70 kg

g = 10 m/s²

∆L = 1,0%L = 0,01L

K = 10¹⁰ A/L

Lei de Hooke:  P = F_elástico  → mg = K_*∆L → 70_*10 = 10¹⁰_*A/L_*0,01L →

700 = 10¹⁰_*A_*0,01 → A = 7x10^-6 → A = 7 μm²

EX-09

A intensidade da força elástica (F), em função das deformações (x) das molas A e B, são dadas pelo gráfico a seguir. Quando um corpo de peso 8 N é mantido em repouso, suspenso por essas molas, como ilustra a figura anexa; calcular a soma das deformações das molas A e B.

Solução:

Primeiramente, vamos calcular as constantes elásticas K_A e K_B das molas:

Do gráfico:

K_A = tgθ = F_A/x_A = 6/3 = 2 N/cm

K_B = tgθ’ = F_B/x_B =  4/5 = 0,8 N/cm

A constante elástica do sistema é:

K_eq = K_A*K_B/(K_A + K_B) = 2*0,8/(2+0,8) = 0,57 N/cm

O corpo está em equilíbrio, portanto,

P = F_mola  → m.g = Keq.∆y, onde Keq = constante elástica do sistema, ∆y = soma das deformações.

Logo,

8 = 0,57. ∆y  → ∆y ≈ 14,0351 cm  → ∆y = 14 cm  

EX-10

A mola da figura tem constante elástica 20 N/m e encontra-se alongada de 20 cm sob a ação do corpo A cujo peso é 5,0 N. Nessa situação de equilíbrio, determinar a indicação da balança, graduada em Newtons.

Solução:

Desenhando todas as forças que atuam no corpo A que está em equilíbrio, tem-se:

Onde

F_B = força de reação da balança (=indicação da balança);

F_M = força elástica da mola;

P = peso do corpo A

Dados:

K = 20 N/m

∆x = 20 cm = 0,20 m

P = 5 N

Portanto,

F_B + F_M = P → F_B = P – F_M  →  F_B = 5 – K.0,2 → F_B = 1 N