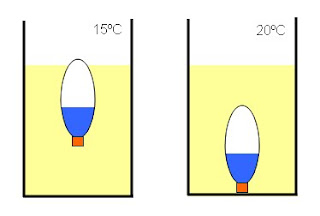
Ex-01 (Olimpíada Paulista de Física-2001)
Quando a temperatura ambiente da sala era de 15ºC, João e
Mário iniciaram um experimento sugerido pelo professor.
Os passos seguidos foram:
1) Colocaram um pouco de água dentro de uma cápsula
de injeção e selaram-na com um pouco de massa epóxi. O peso da cápsula foi
medido como P = 1 N.
2) Puseram a
cápsula no álcool contido num recipiente de 2 litros e observaram que
o objeto não afundava.
3) Mais tarde, quando a temperatura ambiente era de
20ºC, viram que a cápsula começou a afundar e foi parar no fundo do recipiente.
Pergunta-se:
a) Qual a intensidade da força que mantinha a
cápsula flutuando imersa no álcool? Dar as outras características desta força.
b) Por qual razão, quando a temperatura do ambiente
era de 20ºC, a cápsula começou a afundar?
Solução
a) A cápsula está em equilíbrio, então P = E = 1 N
Portanto, a força empuxo E = 1 N (em módulo), direção vertical (mesmo do peso) e sentido para cima (contrário do peso).
b) Com o aumento da temperatura (de 15ºC, para
20ºC), o volume do álcool aumentou, por consequência, sua densidade diminuiu,
pois, d=m/V.
Por
outro lado, considerando que a capsula seja ideal, isto é, o volume é constante com a temperatura (ou
podemos considerar que a variação do
volume da cápsula é desprezível nessa variação
de 5ºC) e massa no interior da cápsula mantém-se igual, logo a densidade da cápsula não se alterou.
Portanto,
a cápsula afundou porque a densidade desta ficou maior que a densidade do álcool.
Ex-02 (Olimpíada Paulista de Física-2001)
Esquematize o desenvolvimento dos procedimentos
experimentais tendo em vista a determinação da densidade relativa da bolinha de
vidro.
Solução
Materiais necessários:
1)
1x Becker 250 ml (graduado);
2)
1x Pipeta com pêra;
3)
1x Proveta 50 ml (graduado);
4)
1x Frasco para compota (40 ml)
5)
Água.
6)
Bolinha de gude (vidro, diâmetro = 12 mm )

Objetivo: obter a densidade da bolinha de gude, aplicando o
conceito de Empuxo, sem utilizar uma balança de precisão.
Procedimentos:
1) Determinar o volume da bolinha de gude.
a) Encher o Becker com água, até a marca de 150 ml
b) Colocar a bolinha de gude no becker com água

a) Medir o volume deslocado da água, utilizando uma
pipeta com pera e uma proveta graduada. Com a pipeta transferir do becker à
proveta a água correspondente ao deslocamento. Transferir a água até que o
nível da água volte à marca de 150 ml.
O
volume lido na proveta é o volume da bolinha de gude.
2) Determinar a massa da bolinha de gude.
Para determinarmos a massa da bolinha, precisamos que ela
flutue na água. Para isso vamos utilizar um frasco para permitir esta
flutuação. Colocar a bolinha de gude no frasco e colocar no becker com
água. Nível de referência é a marca de
150 ml. Para medir o volume deslocado,
idem ao procedimento anterior.
Na condição de flutuação, tem-se:
Logo, precisamos calcular a massa do frasco.
Vamos aplicar o mesmo procedimento anterior para o cálculo
da massa da bolinha:
Colocar o frasco vazio no becker com água. Nível de
referência é a marca de 150 ml.
Na condição de flutuação, tem-se:
3) Calcular a densidade da bolinha de gude.
Temos os valores de massa e volume da bolinha, então, a
obtenção da densidade é imediata:
Ex-03
Um balão de hidrogênio de peso igual a 400 N está preso a um
fio, em equilíbrio estático vertical. Seu volume é 50 m³ . A) Determine o empuxo
devido ao ar no balão, considerando que a densidade do ar é igual a 1,2 kg/m³.
Adote g = 10 m/s². B) Determine a tração
do fio que mantém o balão.
Solução
No balão em equilíbrio atuam seu peso P = 400 N, a tração do
fio T e o empuxo devido ao ar E.
A) O empuxo E é igual ao peso do fluido (ar) deslocado. O volume de ar deslocado é igual ao próprio
volume 50 m³
do balão:
B) Como o balão está em equilíbrio, a resultante das forças
é igual a zero. Logo, P e T equilibram E:
Ex-04
Um sólido flutua em água com 1/8 de seu volume imerso. O
mesmo corpo flutua em óleo com 1/6 de seu volume imerso. Determine a relação da densidade do óleo ρo para a densidade da água ρA.
Solução
Na condição de flutuação:
E (= empuxo) = P (= peso)
Logo tem-se:
Empuxo da água:
Empuxo do óleo:
Igualando:

Ex-05
Um cilindro circular reto, de altura h=30 cm e área da base
A = 10 cm², flutua na água, em posição vertical tendo 2/3 de sua altura imersos.
Aplica-se axialmente na base superior uma força F passando o cilindro a ter 5/6
de sua altura imersos. Determine: A) qual a densidade do cilindro relativa à
água? B) qual a intensidade da força F?
Dados g = 9,8 m/s²; densidade da água = 1 g/cm³.

Solução
A) Na primeira situação só atuam o peso P e o empuxo E.
O volume V é dado pelo produto da área A da base pela altura
h: V = A.h
O volume de água deslocada é o produto da área da base A
pela altura do sólido imerso em água (2/3.h): Va = A.(2/3.h)
Logo:
Na condição de flutuação: P = E:
B) Na segunda situação temos que: F+P = E’ ou F = E’ – P
Portanto:
De item anterior: ρ = 2/3.ρa
Logo:
Ex-06
Um iceberg flutua no mar. A densidade da água do mar é 1,025
g/cm³ e a densidade do gelo que constitui o iceberg é 0,918 g/cm³. Determine a
fração Vi do volume iceberg que permanece imerso em relação ao volume total (V).
Solução
Condição de flutuação:
P = E
Ex-07
Uma jangada de madeira é construída de toras cujo volume é
aproximadamente 100
litros cada. A densidade da madeira é 0,8 kg/l. Três pessoas de 70 kg cada, fazem com que a
jangada fique com 10% de seu volume imerso em água de densidade 1 kg/l. Determine quantas toras compõem a jangada.
Solução
Condição de flutuação:
P = E
Tem-se:
Ex-08 (POLI-SP)
A figura mostra dois corpos A e B de 10 kg de massa cada um,
presos a um fio flexível, inextensível, identificado pelo número 2, que passa por
uma polia de eixo fixo e de massa desprezível. O corpo A tem volume de 10 000
cm³ e está imerso num líquido de densidade 1 000 kg/m³. O fio 1, que mantém inicialmente o sistema em
equilíbrio é cortado num determinado instante. Desprezando a massa dos fios e
considerando a aceleração da gravidade igual a 10 m/s², determine: A) as tensões nos fios 1 e 2, antes de cortar
o fio 1; B) a tensão no fio 2 e aceleração do sistema, logo após o corte do fio
1; C) a tensão no fio 2 e aceleração do sistema após o corpo A sair
completamente do líquido.
Solução
A) Calcular as tensões nos fios antes do corte do fio 1.
Corpo A:
Corpo B:
B) Tensão no fio 2 e aceleração do sistema, logo após o
corte do fio 1:
É intuitivo que o sistema movimenta-se para o lado do corpo
B, isto é, o sentido do movimento é corpo B caindo.
Corpo A:
Corpo B:
C) Tensão no fio 2 e aceleração do sistema após o corpo A
sair completamente do líquido.
Quando
o corpo sai totalmente do fluido o empuxo se torna zero ( E = 0).
Ex-09
Em um recipiente há um líquido de
densidade 2,56g/cm³. Dentro do líquido encontra-se um corpo de volume 1000cm³,
que está totalmente imerso. Qual o empuxo sofrido por este corpo? Dado g=10m/s²
Solução
VFD = volume do fluido deslocado
dF = densidade do fluido
Transformar todos os dados para o Sistema Internacional,
para evitar confusão de unidades:
Cálculo do empuxo sofrido pelo corpo:
Ex-10
Um bloco de massa de 60kg e
densidade de 3,0 *10³ kg/m³ imerso em um líquido de densidade d = 0,90 *10³
kg/m³ e preso por um fio ideal a um dinamômetro. Calcule a intensidade do
empuxo exercido pelo líquido sobre o bloco.
Solução
Primeiramente precisamos encontrar o volume do bloco, o qual
é representado por V.
d = m/V => V = m/d = 60/3,0*10³ → V = 2,0*10-2 m³
A intensidade do empuxo (E) é igual ao peso do líquido
(PF) que caberia no volume ocupado pelo bloco:
E = PF = mF*g = dF*V*g
= (0,90*10³)*(2,0*10-²)*(10) → E =
180N




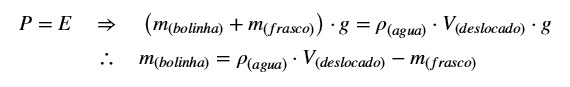













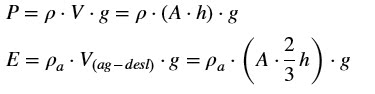



















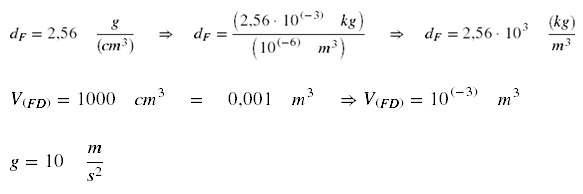

3) Um bloco maciço de densidade de 800kg/m³ e, dimensões: de 0,8 m de largura x 1,2 m de comprimento x 0,5 m de altura: flutua na água. Calcule a altura da caixa que ficará fora da água
ResponderExcluir