Dinâmica - Exercícios Resolvidos - 1

1)   Um ponto material de massa igual a 2Kg está apoiado numa superfície horizontal perfeitamente lisa, em repouso. Uma força constante de intensidade 6 N, paralela ao apoio atua durante 10 s, após os quais deixa de existir.  Determine: A) a aceleração nos 10 s iniciais; B) a velocidade ao fim de 10 segundos; C) considere a origem dos espaços a posição inicial, onde o corpo estava em repouso, calcule a distância percorrida pelo ponto material após 30 segundos.

     

         Solução:

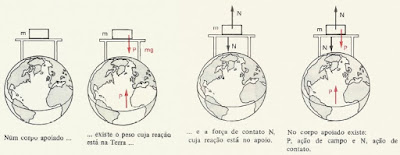
A)  O peso P e a normal N anulam-se verticalmente e por isso, só consideraremos a força F. A força F constante produz a aceleração constante α (MUV).

FR=m.α → F=m.α → 6=2.α → α = 3 m/s²

B)  Ao fim de 10s a velocidade do corpo é:

v = v₀ + αt,  v₀=0,  α=3 m/s²,  t=10s

Logo: v=0+3.10 = 30 m/s → v = 30 m/s

C)  Nos primeiros 10 s → MUV e entre t=10s e t=30s → UM:

I)      s = s0 + v₀t + α.t²/2 → ∆s= v₀t + α.t²/2  

        = 0 + 3.(10)²/2 = 150 m → ∆s = 150 m

II)    v=30m/s (após 10s o corpo continua com MU)  e ∆t=20s

∆_MU = vt = 30.20 = 600 → ∆_MU = 600 m

            Portanto, a distância total percorrida pelo ponto material é:

            ∆s_total = 150 + 600 = 750 m

       Respostas: A) 3 m/s²; B) 30 m/s; C) 750 m

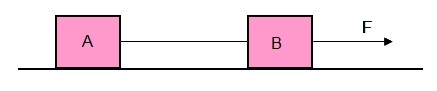
2)   Dois corpos A e B, de massas respectivamente iguais a 2 kg e 3 kg estão apoiados numa superfície horizontal perfeitamente lisa. A força horizontal F=10N constante é aplicada no bloco A. Determine: A) aceleração adquirida pelo conjunto; B) a intensidade da força que A aplica em B.

      Solução:

     A) Para aplicarmos a equação fundamental da dinâmica

 

Devemos analisar as forças que agem em cada bloco.

Em cada bloco, o peso P e a normal N anulam-se verticalmente; por isso,

vamos considerar apenas as forças horizontais, pois a solicitação inicial F

é horizontal. Em A existe a força externa F cuja reação está no agente

externo que a produziu e a força de reação f correspondente à sua ação

de contato em B. Em B existe horizontalmente, apenas a força f ação de

A em B.

A intensidade da resultante das forças em A é (F-f), pois F favorece a

aceleração α e f se opõe.   Em B a resultante é apenas f.

     Com F = 10 N, m_A = 2 kg, m_B = 3 kg temos:

     10 = (2 + 3).α → α = 2 m/s²

B)  A intensidade de f, força de A em B pode ser obtida por qualquer uma das equações (1), ou (2) anteriores.

De equação (2):  f = m_B.α = 3*2 =6 → f = 6 N


Respostas: A) 2 m/s²;  B) 6 N

Observações:

I)   Numa interação deste tipo, o corpo A não transmite a B integralmente a força F; a diferença entre o que recebe e o que transmite resulta em aceleração.

II)   Um cálculo rápido da aceleração pode ser feito considerando A e B como um único corpo; nessas condições a força f não interfere no cálculo pois passa a ser uma força interna. Assim:

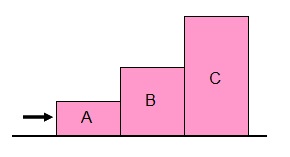
3)  Três corpos A, B e C de massas m_A = 1 kg, m_B = 3 kg e m_C = 6 kg estão apoiados numa superfície horizontal perfeitamente lisa.  A força constante F = 5 N, horizontal, é aplicada ao primeiro bloco A. Determine: a) a aceleração adquirida pelo conjunto; b) a intensidade de força que A exerce em B; c) a intensidade da força que B exerce em C.

Solução:

Como no exercício anterior o peso de cada bloco continua anulado, verticalmente, pela reação normal do apoio.  Para determinação da aceleração, consideremos globalmente o sistema de corpos como um único bloco de massa m_A + m_B + m_C = 10 kg.

Pela equação fundamental da dinâmica:

Para determinar as interações entre os corpos, devemos analisar cada um, separadamente.

Seja f₁ a intensidade da força de A sobre B e f₂, a de B em C.

Respostas:  a) 0,5 m/s²; b) 4,5 N; c) 3 N

4)  Dois corpos A e B de massas iguais a m_A = 2 kg e m_B = 4 kg estão apoiados numa superfície horizontal perfeitamente lisa. O fio que liga A a B  é ideal, isto é, de massa desprezível e inextensível.  A força horizontal F tem intensidade igual a 12 N, constante.   Determine: a) aceleração do sistema; b) a intensidade da força de tração do fio.

Solução:

a)  aceleração do sistema: considerando globalmente os corpos:

F = (m_A + m_B).α  → 12 = (2 + 4).α → α = 2 m/s²

b)  tração do fio: considerando cada corpo.

Pela equação fundamental da Dinâmica para corpo A.

Corpo (A):  T = m_A.α = 2*2 = 4 → T = 4 N

Este resultado poderia, também, ser obtida equacionando-se para o corpo B.

F – T = m_B.α → 12 – T = 4*2 → 12 – T = 8 → T = 4 N

Respostas: a) 2 m/s²; b) 4 N

5) Os corpos A e B da figura tem massas respectivamente iguais a m_A = 6 kg e m_B = 2 kg. O plano de apoio é perfeitamente liso e o fio é inextensível e de peso desprezível.  Não há atrito entre a polia e o fio, considerada sem inércia. Adotar g = 10 m/s².  Determine: a) a aceleração do conjunto; b) a tração do fio.

a) Considerando separadamente cada corpo:

Em A, a força normal N_A anula a ação do Peso, pois não há movimento vertical. Pela equação fundamental da dinâmica:

T = m_A*α, com m_A = 6 kg → T = 6α (Eq-01)

Considerando o corpo B:

Sua aceleração é a mesma de A pois o fio é ideal (inextensível e massa desprezível): no mesmo intervalo de tempo A e B percorrem as mesmas distâncias e atingem a mesma velocidade.

O peso P_B provoca α e a tração T opõe-se a α; daí, pela equação fundamental, temos:  

P_B – T = m_B*α, m_B = 2 kg → P_B – T = 2α (Eq-02)

Substituindo a (Eq-01) em (Eq-02) temos:

T = 6α em P_B – T = 2α → P_B – 6α = 2α → 2*10 = 2α + 6α  → 8α = 20

→ α = 2,5 m/s²

Substituindo este valor de α na (Eq-01):

T = 6α → T = 6*2,5 = 15 N → T = 15 N

Respostas: a) α = 2,5 m/s²; b) T = 15 N

Observação:

Podemos calcular a aceleração, considerando A e B como um único bloco.

F_R = P_B →  m_(A+B)α = m_B.g

Assim, se (m_A + m_B) é a massa do conjunto, temos:

6)  No arranjo experimental da figura os corpos A, B e C têm massas respectivamente iguais  a m_A = 5 kg, m_B = 2 kg e m_C = 3 kg.  A aceleração da gravidade local é 10 m/s². Os fios são idéias (=inextensíveis e massa desprezível); não há atritos entre fios e as polias. O plano horizontal é perfeitamente liso. Determine: a) a aceleração do sistema de corpos; b) as trações nos fios.

Solução:

O peso de B é anulado pela reação normal do apoio; porém os pesos P_A e P_C são forças externas ativas. P_A é maior que P_C:

Se o sistema partir do repouso, o corpo B move-se da esquerda para a direita, pois, o peso de A é maior que o de C.

O peso P_A favorece a aceleração e P_C se opõe. Pela equação fundamental da dinâmica aplicada ao conjunto de corpos de massa total (m_A + m_B + m_C) vem:

Para a determinação das trações nos fios, consideremos cada corpo. No caso há duas trações pois temos dois fios. Assim:

Como já temos a aceleração α bastam duas dessas equações para a determinação das trações. De (Eq-1) e (Eq-2), por exemplo, temos:

Respostas:  a) 2 m/s²;     b) T1=40N;    c) T2=36N

7)  Um homem de 70 kg está na cabina de um elevador que desce acelerado na razão de 2 m/s². Considere o homem apoiado numa balança, na escala calibrada em newtons.  Determine a intensidade da força indicada na balança.  Adotar g = 10 m/s2².

Solução:

O elevador desce verticalmente com aceleração α=2m/s² em relação a um Observador Externo em repouso no solo. Este observador externo, que é um referencial inercial, vê atuarem no homem, as forças P, ação da Terra e N, ação da balança no homem.  O homem atua na balança, exercendo a força de intensidade N, que é a indicação, pois está calibrada em forças.

A resultante das forças que atuam no homem é F_R = P – N; logo:

Resposta:

A indicação da balança é 560 N

8)  No arranjo experimental da figura, A e B têm massas respectivamente iguais a 6 kg e 2 kg.  Os fios e as polias têm massas desprezíveis. Não há atritos entre o fio a polia. Determinar: a) a aceleração do conjunto; b) as trações nos fios. Considere que o sistema partiu do repouso e adote g=10 m/s².

O arranjo experimental é conhecido como máquina de Atwood (1745-1807), físico inglês, que com um arranjo deste tipo estudou a queda dos corpos.

a) O corpo A desce enquanto B sobe, pois o peso de A é maior que o de B.

Para o conjunto de corpos de massa total (m_A + m_B), o peso P_A favorece a aceleração e P_B se opõe:

b) Vamos calcular a força de tração no fio que liga A a B.

Qualquer uma das equações anteriores nos fornece T.

Vamos tomar a (eq-2):

A tração T1 no fio que liga o eixo da polia ao teto pode ser obtida como se segue: 

A polia não possui peso e seu eixo está em equilíbrio. Deste modo a resultante das forças é nula.

Respostas:  a) α = 5 m/s²;   b) 30 N e 60 N

9) Determine a força que o homem deve exercer no fio para manter em equilíbrio estático o corpo suspenso de 360 N. Os fios são considerados inextensíveis e de massas desprezíveis; entre os fios e as polias não há atrito. As polias são ideais, isto é, não possuem massa.

Solução:

Para haver equilíbrio, a resultante da força deve ser nula. No corpo suspenso, a tração T é igual ao peso P = 360 N, pois não há aceleração. A distribuição de trações é como indicam as figuras a seguir:

Resposta: 45 N

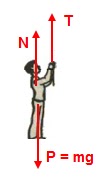
10) O sistema esquematizado compõe-se de um elevador de massa M e um homem de massa m. O elevador está suspenso a uma corda que passa por uma polia fixa e vem às mãos do operador; a corda e a roldana são supostas ideais. O operador puxa a corda e sobe com aceleração constante α, juntamente com o elevador. São supostos conhecidos M, m, α e g. Determine a força que a plataforma exerce no operador.

Solução:

Considerando o sentido da aceleração α como positivo, vamos isolar os corpos, identificando todas as forças que atuam sobre eles:

Homem:

P = peso do homem;

T = reação ao puxão que o homem dá na corda;

N = reação do elevador sobre o homem (força a determinar).

Como só há movimento na direção vertical, então temos que:

T + N – P = m.α  (Eq-1)

Elevador:

Pc = peso da cabina do elevador;

T = ação devido ao puxão que o homem dá na corda;

N = ação do homem sobre o elevador.

Então temos que:

T – (N + Pc) = M.α  (Eq-2) 

Podemos observar que as (Eq-1) e (Eq-2) formam um sistema de duas equações a duas incógnitas (T e N).

Como o objetivo é encontrar o valor de N; vamos subtrair (Eq-2) de (Eq-1):

Dinâmica

1) Introdução

É a parte da Mecânica que estuda os movimentos e suas causas.

A equação fundamental da dinâmica:

(Eq-01)

Esta equação é uma síntese dos princípios da mecânica clássica proposta por Isaac Newton e com ela, muitos fenômenos podem ser explicados dentro de uma boa aproximação.

  

• Massa é uma grandeza escalar associada à quantidade de matéria do corpo.

• Força é uma grandeza vetorial, pois produz variação de velocidade, que é vetorial.

A variação de velocidade no tempo determina a aceleração; daí decorre que uma força aplicada num ponto material provoca uma aceleração.

Em Dinâmica, forças são os agentes que produzem as variações de velocidade de um corpo.

2) Equilíbrio

Há 2 tipos básicos de equilíbrio.

a)     a velocidade vetorial é constante nula com o tempo: o ponto material está em repouso num determinado referencial. O repouso é chamado Equilíbrio Estático.

b)     A velocidade vetorial é uma constante com o tempo e não nula: o ponto material tem movimento retilíneo e uniforme (MRU) pois sua velocidade é constante em módulo, direção e sentido.  O MRU é chamado Equilíbrio Dinâmico.

Resumindo:

O conceito de equilíbrio é relativo ao referencial. Por exemplo, um carro em movimento acelerado em relação ao solo, não está em equilíbrio, pois possui aceleração.  Porém, um passageiro em repouso em seu interior está em equilíbrio estático em relação ao carro.

Diz-se que um ponto material está em repouso, ou em movimento retilíneo e uniforme.

Inércia é a propriedade geral da matéria de resistir a qualquer variação em sua velocidade. Um corpo em repouso tende, por inércia, a permanecer em repouso; um corpo em movimento tende, por inércia, a continuar em movimento retilíneo e uniforme (MRU).

3. Força

Forças são interações entre corpos que produzem variações em sua velocidade, isto é, provocam aceleração.

Podem existir forças quando corpos entram em contato (pé do jogador de futebol chutando a bola), ou mesmo quando estão à distância (a Terra atraindo um corpo em queda livre).

Newton estabeleceu uma lei básica para a análise geral das causas dos movimentos, relacionando as forças aplicadas a um ponto material de massa m constante e as acelerações que provocam.  (Princípio Fundamental da Dinâmica).

A lei de Newton estabelece que a resultante das forças aplicadas a um ponto material é igual ao produto de sua massa pela aceleração adquirida:

(Eq-02)

É Equação Fundamental da Dinâmica.

A equação (Eq-02) deixa de ser válida se a massa da partícula variar, fato que ocorre no domínio microscópico das partículas atômicas. Nos fenômenos macroscópicos de nossa vida cotidiana, a Equação Fundamental da Dinâmica é suficiente para interpretações e análises.

4. Peso (é uma força)

Os corpos próximos à superfície da Terra são atraídos por ela. Abandonados a uma determinada altura do solo, caem sofrendo variações de velocidade.

Peso de um corpo é a força de atração que a Terra exerce no corpo.

Desprezada a ação do ar, a única força atuante sobre o corpo em queda livre é seu peso.

Portanto,

MASSA NÃO PODE SER CONFUNDIDA COM PESO.

Quando desprezamos a resistência do ar e num mesmo local da Terra, CORPOS DIFERENTES (de massas e pesos diferentes) caem juntos; em outras palavras, partindo de mesma posição, atingem o solo no mesmo instante.

5. Classes de forças

Forças de contato: são forças que existem quando duas superfícies entram em contato.  Por exemplo: quando empurramos um bloco contra uma parede, há forças de contato entre bloco e a parede.

Forças de campo: são forças que os corpos exercem mutuamente ainda que estejam distantes um do outro.  Por exemplo: a Terra atrai corpos que estão próximos à superfície exercendo neles forças de campo.

6. Princípio da Ação e Reação

Aplicações (exemplos)

Um corpo próximo à superfície da Terra é atraído por ela.  A terra exerce nele uma força peso; pelo princípio de ação e reação, o corpo, também exerce na Terra uma força , da mesma intensidade. Mesma direção e sentido contrário.

Um corpo apoiado numa superfície horizontal, como uma mesa. 

Um corpo suspenso por um fio inextensível e sem peso (peso do fio desprezível).

7. Princípios de Newton da Dinâmica Clássica

7.1) 1ª Lei de Newton – Princípio da Inércia:

Um ponto material isolado está em repouso, ou em movimento retilíneo e uniforme.

7.2) 2ª Lei de Newton – Princípio Fundamental:

A resultante F_R das forças aplicadas a um ponto material é igual ao produto de sua massa m pela aceleração adquirida a.

7.3) 3ª Lei de Newton – Princípio da Ação e Reação:

Toda vez que um corpo A exerce um força F_A num corpo B, este também exerce em A uma força F_B, tal que, 

isto é, as forças têm mesma intensidade e direção, mas, sentidos opostos.

8. Críticas à Mecânica Clássica

As leis de Newton constituem os fundamentos da Mecânica Clássica. Dão uma boa aproximação quando aplicadas para interpretar muito fenômenos da vida cotidiana. Para a Engenharia, são bastante adequadas.

De acordo com a teoria da relatividade de Einstein (1879 – 1955), a massa é função da velocidade, fato que Newton desconhecia. Porém, para velocidades bem inferiores à da luz, podemos considerar a massa praticamente constante e válida, a equação fundamental da Dinâmica.

Ainda pela relatividade sabemos que nenhuma informação pode ser transmitida com velocidade superior à da luz no vácuo. Daí, o princípio da ação e reação é falho quando aplicado às forças de campo à longa distância. Os pares ação-reação não são simultâneos, levando um determinado tempo para propagação da interação. Esse fato não foi discutido por Newton. Mesmo assim, trabalhamos com esse princípio e os demais da Mecânica Clássica de Newton, pois eles continuam válidos para o comportamento macroscópio e global da matéria