1) Um corpo é lançado na vertical, de baixo para
cima, com velocidade inicial de 49 m/s, em local onde g=9,8 m/s². Calcule o tempo total gasto pelo corpo para
voltar ao ponto de partida e sua velocidade ao chegar ao mesmo.
2) Um observador situado no topo de um prédio de 44,8 metros de altura
vê passar, para cima, e 4 segundos após para baixo, um corpo lançado
verticalmente na base do edifício.
Determinar a altura máxima
alcançado pelo corpo e o módulo da velocidade de lançamento. Considerar:
g = 10 m/s²
3) Um corpo animado de MRUA tem num determinado
instante a velocidade de 8 m/s.
Decorridos 10 segundos, sua velocidade torna-se igual a 28 m/s. Calcule a aceleração do corpo.
4) Dois automóveis partem de duas cidades A e B em
horários diferentes. A distância entre A
e B é 300 Km . As velocidades dos dois carros são uniformes
e de sentidos contrários. VA = 50 Km/h e VB = 100 Km/h . Os tempos de partida são respectivamente tA
= 12:00h e tB = 13:00h. Desenhe o
gráfico que representa os movimentos dos dois veículos, tomando-se como origem
do sistema de referência a cidade A.
5) Um macaco que pula de galho em galho em um
zoológico, demora 6 segundos para atravessar sua jaula, que mede 12 metros . Qual a velocidade
média dele?
6) Um carro viaja de uma cidade A a uma cidade B,
distantes 200km. Seu percurso demora 4 horas, pois decorrida uma hora de
viagem, o pneu dianteiro esquerdo furou e precisou ser trocado, levando 1 hora
e 20 minutos do tempo total gasto. Qual foi a velocidade média que o carro
desenvolveu durante a viagem?
7) Durante uma corrida de 100 metros rasos, um
competidor se desloca com velocidade média de 5m/s. Quanto tempo ele demora
para completar o percurso?
8) É dado o movimento s = 100 + 80t, onde s →
m, t →
s. Determine:
a)
O espaço inicial e a velocidade;
b)
O espaço quando t = 2s;
c)
O instante em que o móvel se encontra a 500 m da origem de espaço;
d)
O sentido do movimento (progressivo, ou
retrógrado)?
9) É dado o movimento s = 60 – 12t, onde s →
km, t →
h. Determine:
a)
O espaço inicial e a velocidade;
b)
O espaço quando t = 3h;
c)
O instante em que o móvel passa pela origem de
espaços;
d)
O sentido do movimento (progressivo, ou
retrógrado)?
10) Um ponto
material possui velocidade constante de valor absoluto 70 Km/h , e se movimenta em
sentido oposto ao da orientação positiva da trajetória. No instante t = 0 h, esse ponto passa pelo
marco igual a 420 Km
da origem de espaços na trajetória.
Determine:
a) A equação horária;
b) O instante em que o móvel passa pela origem de
espaços.
11)
Dois
móveis percorrem a mesma trajetória e suas posições estão medidas a partir do
marco escolhido na trajetória. Suas funções horárias são:
a)
SA= 30 –
80t
b)
SB = 10 +
20t
Onde
t = tempo em horas e o SA e SB são posições em
quilômetros. Determine
o instante e a posição do encontro.
12)
Dois
móveis P1 e P2 caminham na mesma trajetória e no instante em que se dispara o
cronômetro (t=0) suas posições são:
Os sentidos de seus movimentos
estão indicados na figura e suas velocidades
(em valor absoluto) são respectivamente iguais a v1 = 20 m/s e v2 = 10 m/s. Determine o instante
e a posição de encontro dos móveis.
13) Duas cidades A e B estão separadas pela
distância de 300 Km ,
medidos ao longo da estrada que as liga.
No mesmo instante, um móvel P passa por A, dirigindo-se a B, e outro móvel Q passa por B, dirigindo-se a A.
Seus movimentos são uniformes e suas velocidades (em valor absoluto) são
iguais a 80 Km/h
(P) e 70 Km/h
(Q). Determine:
a)
O instante do encontro;
b)
A posição de encontro.
14) Determinar o intervalo de tempo (em minutos)
para a luz vir do SOL à TERRA. No vácuo, a velocidade da luz é constante e
aproximadamente igual a 3,0 x 105 km/s. A distância entre o Sol e a Terra é de
1,49x108 km. Considere o
movimento de propagação da luz como retilíneo e uniforme.
15) Durante
uma tempestade, um indivíduo vê um relâmpago, mas, ouve o trovão 5 segundos
depois. Considerando-se o som no ar, com velocidade praticamente constante e
igual a 340 m/s, determine: A) a distância que separa o indivíduo e o local do
relâmpago; B) o tempo que a luz levou para ir do local onde foi produzido o até
onde está o indivíduo. A velocidade da
luz é aproximadamente igual a 300 000 km/s.
16) A
velocidade de projeção de um filme sonoro é constante e na razão de 24
fotografias projetadas em cada segundo na tela. Quantas fotografias são
projetadas na tela durante a projeção de um filme que dure 2 horas.
17) A
velocidade média de um móvel na metade de um percurso é 30 km/h e esse mesmo
móvel tem a velocidade média de 10 km/h na metade restante desse mesmo
percurso. Determine a velocidade média
do móvel no percurso total.
18) Dois
trens P e Q percorrem trajetórias retilíneas e paralelas. O trem P possui 30 m de comprimento e
velocidade de 30 km/h e o trem Q possui 50 m e 10 km/h; seus movimentos são uniformes. Determine: a) o intervalo de tempo da ultrapassagem, isto é, o
intervalo de tempo necessário para que o trem mais veloz P ultrapasse o trem mais
lento Q; b) o espaço percorrido por P durante a ultrapassagem.
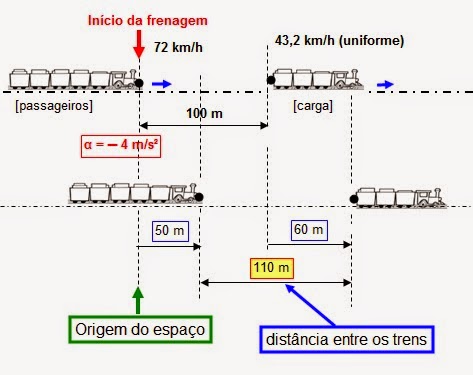
19) O
maquinista de um trem de passageiros vê a sua frente, na mesma linha férrea e
caminhando no mesmo sentido, um trem de carga.
Para evitar um desastre, o maquinista aciona os freios causando um
retardamento constante de 4 m/s² (em módulo). No instante que acionou os
freios, a velocidade do trem de passageiros era 72 km/h, e o mesmo estava a 100
m do trem de carga. O movimento do trem
de carga é uniforme, com velocidade igual a 43,2 km/h. Determine: a) se há colisão dos trens; b) se não houver, qual a distância que os separa, no instante em que
o trem de passageiros pára.
20) A distância da TERRA a LUA é aproximadamente 3,84x108 m. Admita a Terra e
Lua estacionárias no espaço e considere um foguete que segue trajetória
retilínea da Terra à Lua, com velocidade constante de 1,52x10³ m/s. Determine o tempo de duração do trajeto em
segundos e em horas.
R1)
Desprezando a
influência do ar: a velocidade com que o corpo retorna ao ponto de partida
é a mesma da velocidade de lançamento, portanto, igual a 49 m/s.
Vamos calcular o tempo total: t = ts + td, mas ts = td, então, t = 2*ts
Sabemos que a expressão que descreve a velocidade é: v = vo +
αts = vo
–gts, logo, 0 = 49 – 9,8ts → ts =
5 s.
Portanto, o tempo total de ida e volta = t = 2*ts = 2*5 =10 → t = 10s
R2)
Dados: g = 10 m/s², h1=44,8 m
ts = tempo de subida, td = tempo de descida e ts=td=t
ts + td =
4s → 2t = 4 → t = td
= ts = 2s
Fazendo o desenho do problema:
Descida: h2=?, vo = 0, g= +10m/s² (g é positivo porque sentido para baixo)
h2 = (h2)0 + vo.t + g.t²/2 → h2 = g.t²/2 = (+10).2²/2 = 20
m
Como as distâncias de subida e descida são iguais, em
relação ao observador no topo do prédio:
A altura máxima: hmax = h1 +
h2 = 44,8 + 20 = 64,8 m → hmax = 64,8
m
Aplicando a fórmula de Torricelli:
Temos os seguintes dados:
v = 0, α = -g = -10 m/s², ∆s = hmax = 64,8 m
Portanto: 0 = vo² +2.(-g).hmax ↔ - vo² = - 2.g.hmax → vo = √ 2.g.hmax
vo = √
2.10.64,8 = √ 1296 → vo = 36 m/s
R3)
Dados (=informados):
V0 = 8 m/s, V = 28 m/s e ∆t = 10
s. α = ?
V = V0 + α.∆t → 28 =
8 + α.10 → 10α = 20
→ α = 2 m/s²
R4)
Foram dados:
a)
distância entre A e B = 300 Km
b)
velocidades constantes porém sentidos
contrários: VA=50 Km/h e VB=100 Km/h
c)
Carro (A) parte aos 12:00h
d)
Carro (B) parte aos 13:00h
Vamos calcular os tempos que cada carro leva para fazer os 300 Km de distância entre
cidades A e B.
1)
Carro que sai de A = 50 Km/h → ∆t = 300/50 = 6h
2)
Carro que sai de B = 100 Km/h → ∆t = 300/100 =
3h
A origem do sistema de referência é a cidade A.
Então o gráfico é:
R5)
S=12mt=6s
v=?
R6)
S=200km
t=4h
v=?
Vm = ∆S/∆t = 200Km/4h =
Mesmo o carro tendo ficado parado algum tempo durante a viagem, para o cálculo da velocidade média não levamos isso em consideração.
R7)
Vm = ∆S/∆t → ∆t = ∆S/Vm = 100m/5m/s = 20 s → Vm = 20 s
R8)
a) S = 100 + 80*t
S = S0
+ V*t
Comparando as duas expressões: S0 = 100
m e V = 80 m/s
b) t = 2s →
S = 100 + 80*2 = 100 + 160 = 260
→ S = 260
m
c) S = 500m
500 = 100 +80*t → 80*t = 400
→ t = 5 s
d) O movimento é progressivo, porque a velocidade é positiva e a posição
aumenta com o tempo.
R9)
a) S = 60 – 12*t
(S→Km, t→h)
S = S0
+ VT
Comparando as duas equações: S0 = 60 Km , V = -12 Km/h
b) T = 3 h
S = 60 – 12*t → S =
60 – 12*3 = 24 → S = 24 Km
c) Instante (t=?) quando passa pela origem de
espaços (S0 = 0):
S = 60 – 12*t → 0 =
60 – 12t → 12t = 60
→ t = 5 h
d) O movimento é retrógrado porque a velocidade é negativa e a
posição diminui com o tempo (está contra o sentido positivo da trajetória).
R10)
a) MU -
S = So + Vt
So
= 420 Km
e
V=
-70 Km/h
(negativo porque está se movendo no sentido contrário ao sentido positivo da trajetória).
Logo,
a equação horária é: S =
420 – 70t (S → Km, t → h)
b) t=?, quando passa na posição zero (S=0)
S
= 420 – 70t
0
= 420 – 70t → t = 6 h
R11)
(t→h, SA e SB→Km)
SA = 30 – 80t
SB = 10 + 20t
t = 0, temos SA = 30 Km , SB = 10 Km
Instante do encontro:
SA = SB → 30 – 80t = 10 + 20t →
- 100t = -20 → t = 0,2 h
Posição do encontro:
SA = SB → SB
= 10 + 20t → SB =10 + 20*0,2 → SA = SB = 14 Km
R12)
Pelo desenho obtemos as equações horárias:
Móvel-1: S(1) = 15 +
20t
Móvel-2: S(2) = 45 –
10t
Instante do encontro:
S(1) = S(2) → 15
+ 20t = 45 – 10t →
t = 1 s
Posição do encontro:
S(1) = S(2) → S(1) = 15 + 20t = 15 + 20*1 = 35 m → S(1) = S(2) = 35 m
R13)
Trata-se de um Movimento Uniforme:
Colocando em desenho os dados fornecidos.
As equações horárias são ( S →
Km, t → h):
1)
S(P) = 80t
2)
S(Q) = 300 – 70t
a)
No encontro S(P) = S(Q)
80t
= 300 – 70t → 150t = 300 →
t = 2 h
b)
Posição de encontro S(P) = S(Q).
S(P)
= 80t = 80x2 = 160 Km → Posição de encontro: 160
Km de A.
R14)
O movimento é uniforme:
s = s0 +vt
Como consideramos S0=0,
a origem de espaços no SOL: s = vt
Portanto: t = s/v =
1,49x108 /3x105 = 497 → t =
497 s
Para o tempo em minutos é só dividirmos por 60, porque 1 min
= 60 s:
t =
497/60 ≈ 8min 17s
R15)
A
LUZ é muito mais veloz que o som:
Assim, uma pessoa vê o relâmpago quase no mesmo instante de
sua produção, mas, só ouve o som do trovão alguns segundos depois.
Vamos considerar que a velocidade do som no ar é constante e
o movimento de propagação é uniforme (portanto: MU, s = s0 + vt).
A origem dos espaços na origem do relâmpago: s(som) = vt.
s(som) = 340*5 = 1700 m → s(som) = d = 1,7
km (distância que separa o indivíduo do local da
origem do relâmpago).
Para LUZ:
s(luz) = v(luz).t(luz) →
t(luz) = s(luz)/v(luz) = 1,7/300000 ≈
5,7 x 10-6 s
t(luz) ≈ 5,7 x 10-6 s = 5,7 μs (microsegundos)
R16)
Um pouco de biologia
humana: Quando um raio luminoso atinge a retina de nossos olhos, produz uma
sensação luminosa que dura um décimo de segundo, depois que o raio deixou de
existir. O movimento de personagens e
objetos que enxergamos na tela de um cinema deve-se a essa particularidade de
nossa retina.
Uma fotografia é projetada na tela durante um tempo muito
curto (aproximadamente, 0,04 s, pois em um segundo são projetadas 24
fotografias), mas suficiente para impressionar nossa retina; logo é substituída
por outra, ainda que em nosso olho persista a anterior, e assim sucessivamente. Para nosso olho, essa sucessão nos dá o
efeito da visão de um movimento contínuo.
Agora vamos a resolução do problema:
Como a velocidade de projeção é constante (24 fotografias
por segundo), o movimento é uniforme (MU).
Logo, podemos aplicar a fórmula: s = vt, sendo v=velocidade,
número de fotografias por segundo; t=tempo em segundos e s=número de
fotografias.
Para t=2h = 2 * 60 * 60 = 7200 s
s = vt
= 24*7200 = 172.800 fotografias
R17)
Desenhando o que foi descrito no texto do problema, temos:
A velocidade média do móvel no percurso total:
v = 2d / (t1
+ t2)
Calculando os tempos t1 e t2:
t1 = d / 30 e t2 = d / 10 → (t1
+ t2) = d/30 + d/10 = 4d/30
Logo,
v = 2d / (t1
+ t2) = 2d / (4d/30) = 60d/4d = 15 → v = 15 km/h
A velocidade média no percurso AB é 15 km/h . Note que não é
igual à média aritmética das velocidades médias em cada trecho do percurso,
pois não se trata de MUV.
a)
Calculando o tempo (em segundos) de
ultrapassagem:
Pela figura observamos que: O
ponto P se aproxima do ponto Q na velocidade (relativa) de 20 km/h ; e alcança o ponto
Q após percorrer 80 m
(=soma dos comprimentos dos trens).
s = v.t →
0,080 = 20.t → t = 0,080/20 = 0,004 h → t = 0,004 * 3600 = 14,4 → t = 14,4 s
b)
Calculando o espaço percorrido pelo trem P.
(adotando s0 = 0,
origem dos espaços, onde inicia a ultrapassagem (A))
s = s0 + v.t → s =
30*0,004 = 0,12 km
→ s = 120
m
Desenhando a situação do problema com os dados informados:
Vamos calcular primeiramente, o tempo gasto pelo trem de
passageiros (até a parada total); e a distância percorrida.
A origem dos espaços: posição onde o trem de passageiros
inicia a frenagem.
Trem de
Passageiros (MUV):
s = s 0 + v0.t + α.t²/2; v = v0
+ αt; s 0 = 0 e v0
= 72 km/h
(= 72: 3,6 = 20 m/s)
v = v0 + αt
→ 0 = 20 – 4t → t = 5 s (para a parada
total)
s = s 0 + v0.t + α.t²/2 → s = 0 + 20*5 – 4*5²/2 = 50 m → s = 50 m (até a parada total)
Trem de Cargas (MU):
Vamos calcular quanto o trem de cargas anda, até a parada
total do trem de passageiros. (t = 5 s, 43,2 km/h = 12 m/s, s
0 = 100 m )
s = s 0 + v.t
→ s = 100 + 12*5 = 60 → s = 160 m
Não há
colisão entre os trens; vejamos as posições finais dos trens, após a parada
total do trem dos passageiros:
O trem
de passageiros andou 50
metros até parar totalmente e gastou 5 segundos. Enquanto que o trem de cargas andou 60 metros nos mesmos 5
segundos. Portanto, a distância entre os trens, quando o trem de passageiros
parou é de 110 metros . Logo, não há colisão.
Movimento do foguete é uniforme, portanto,
s = s0 + v*t , s0 = 0 (pois, vamos
adotar que a origem de espaços é a Terra).
3,84x108 = 1,52x10³*t → t =
3,84x108 / 1,52x10³ = 2,52x105 segundos
Para obtermos o tempo, em horas, basta dividirmos por 3600:
t = 2,52x105 / 3600 = 70 horas
Logo, não há colisão.