Determinar as
trações nos fios ideais AB e BC, sabendo-se que o sistema está em equilíbrio na
posição indicada.
Dados: senθ =
0,6; cosθ = 0,8; P = 90 N
Solução
Isolando o ponto B, onde se
encontram os três fios. É fácil ver que a tração no fio vertical (direção y) é
o peso P = 90 N.
Por conveniência vamos
iniciar na direção y (vertical):
Na direção x:
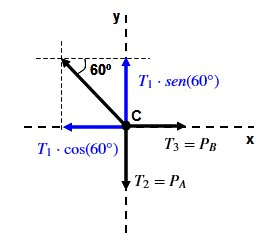
Para o sistema da figura, em
equilíbrio, qual a relação entre os pesos PA e PB dos
corpos A e B? Os fios e as polias são ideais.
Solução:
Ponto C (ponto
de concorrência dos 3 fios):
Observa-se que a tração no
fio vertical é igual ao peso do corpo A (PA) e no fio horizontal
igual ao peso do corpo B (PB); pois o sistema está em equilíbrio.
Projeção na direção x
Projeção na direção y:
Dividindo-se, membro a
membro (2) por (1), tem-se:

O esquema anexo
representa um sistema em equilíbrio e na iminência de movimento. Determine o
coeficiente de atrito μ entre o corpo A e o plano horizontal. Os fios são
ideais. São dados os pesos dos corpos A e B: PA=200N e PB=100N;
senθ=0,8 e cosθ=0,6.
Solução
Balanço
de forças no corpo A e no ponto C:
Corpo A
está em equilíbrio, então:
como o corpo está na
iminência de movimento, podemos escrever que:
Ponto C
está em equilíbrio, então:
Projeção na direção x:
Projeção na direção y:
Dividindo-se, membro a
membro, (2) por (1), tem-se:
De (1), sendo T=μ.PA,
vem:
No sistema esquematizado,
em equilíbrio, determine as trações nos fios ideais AB e BC. Dados: senα
= 0,8; cosα =
0,6; (α + β) = 90º
Solução:
Ponto B: (neste ponto os
três fios concorrem).
Dados:
senα = 0,8
cosα = 0,6
α + β = 90º (α e β) são ângulos complementares, então é
verdade que:
senβ = cosα = 0,6
cosβ = senα = 0,8
Projeção na direção x
(horizontal):
Projeção na direção y
(vertical):
No sistema em
equilíbrio, do desenho, o fio BC deve permanecer horizontal. Os fios e a polia
são ideais. Sendo M1 = 3
Kg e g = 10 m/s² determine:
Sistema está em equilíbrio,
então o ponto B está em equilíbrio.
Projeção na direção x
(horizontal):
A
tração BC é igual a P1 = 3.10 = 30 N

Projeção na direção x
(horizontal):
A tração BC é igual a P1
= 3.10 = 30 N
Uma corda AB tem
a sua extremidade A fixa, enquanto que a outra B está ligada ao bloco M em
forma de paralelepípedo de peso 120 N. Este bloco repousa sobre um plano
horizontal. O coeficiente de atrito entre o plano e o bloco é 0,30. Em um ponto
C da corda é dependurado um peso Q tal que o ângulo formado pelo trecho AC com
a horizontal seja 60º; o trecho CB é horizontal.
A) Qual a força
de atrito exercida pelo plano sobre o bloco quando o mesmo estiver na iminência
de movimento? B) Qual o peso máximo que
se pode pendurar em C? Adotar g=10 m/s².
Solução
Balanço de forças de tração
no Ponto C (3 forças concorrem neste ponto) :
O sistema está em equilíbrio
na condição de iminência do movimento.

A) Força de atrito estático:
Esta força de atrito é
máxima, porque o corpo M está na iminência de movimento.
A força de tração CA é
máxima, para que o sistema permaneça em equilíbrio.

O corpo
representado na figura tem peso 40 N. Ele é mantido em equilíbrio por meio do
fio ideal AB de comprimento 50
cm e pela ação da força horizontal F. Sabendo-se que a
distância BC é igual a 30 cm,
determine a tração no fio e a intensidade da força F.
Solução
Balanço de forças no Ponto
B:
Projeção na direção y:
A distância AC = 40 cm ( terno de Pitágoras,
(3,4 e 5))
Projeção na direção x:
Uma corda de
comprimento ℓ
= 7,0 m está atada a dois pontos A e B situados na
mesma horizontal e a distância d = 5,0 m. Num ponto D da corda, a 3,0 m de A, prende-se um
corpo de peso P = 10 kgf. Calcule as forças tensoras nos trechos AD e BD da
corda.
Solução
Colocando
em desenho as informações que são fornecidas:
Nota-se que o triângulo ABD
é retângulo, terno de Pitágoras (3,4,5).
Projeção
na direção x (horizontal):
Projeção na direção y (vertical):
Por substituição: (1) em (2)
Em (1):
Um corpo de peso
P = 50 N está apoiado num plano inclinado de 30º com a horizontal. O
coeficiente de atrito estático entre o corpo e o plano é μ = 0,2. Um segundo
corpo de peso Q está preso ao primeiro por meio de um fio que passa por uma
polia sem atrito. Entre que limites pode variar o peso Q de forma que o sistema
permaneça em repouso? Poderá ser nula a
força de atrito entre o corpo e o plano inclinado? Justifique. Dados sen30º =
0,5; cos30º = 0,87.
Solução
Lembrando que a força de
atrito sempre se opõe ao movimento.
Na iminência de descer,
temos que:
Na iminência de subir, temos
que:
Portanto,
Para Q menor que 16,30 N o
corpo desce e para Q maior que 33,70 N o corpo sobe, logo, o Q pode assumir os
seguintes valores para que o sistema permaneça em repouso:
Sim, a força de atrito pode ser nula, desde que
O esquema
representa um sistema em
equilíbrio. Sabe-se que o peso P do corpo apoiado sobre o
plano inclinado é 200 kgf e P1 = 20 kgf. Desprezando as forças de
atrito na polia e no plano, calcular a reação R do plano sobre o corpo.
Solução
Projeções das forças de
tração na direção y:
O sistema está em
equilíbrio, então,