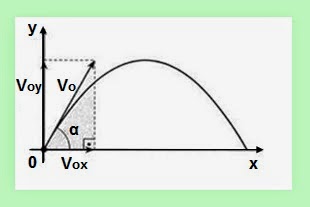
Cálculo da altura e distância horizontal para lançamento a α graus em relação à horizontal.
Da figura temos que:
Voy = Vo. senα
Vox = Vo. cosα
a) Movimento vertical – Nesse movimento, a velocidade é variável, pois o corpo está sujeito à aceleração da gravidade: na subida, o movimento é retardado (velocidade e aceleração têm sentidos contrários); na descida, o movimento é acelerado (velocidade e aceleração têm sentidos iguais).
No ponto mais alto da trajetória, podemos dizer que a componente vertical da velocidade do foguete, automaticamente, irá se anular; e a velocidade irá diminuir à componente horizontal.
Vy = Vo . senα – g.t
No ponto mais alto, temos que Vy = 0 e t = tsubida
Logo:
0 = Vo.senα – g.ts
No ponto mais alto da trajetória, podemos dizer que a componente vertical da velocidade do foguete, automaticamente, irá se anular; e a velocidade irá diminuir à componente horizontal.
Vy = Vo . senα – g.t
No ponto mais alto, temos que Vy = 0 e t = tsubida
Logo:
0 = Vo.senα – g.ts
Portanto,
b) Movimento horizontal – Esse movimento é uniforme, uma vez que Vox é constante (desprezando-se a resistência do ar).
É importante lembrar que: O alcance é mesmo para diferentes corpos, lançados com a mesma velocidade inicial e com ângulos de lançamento complementares (aqueles cuja soma vale 90°).
O tempo total é igual a:
tempo de subida + tempo de queda (=descida)
(Movimento Uniforme, Velocidade constante)
Fatos:
1) Podemos notar que D é máximo, quando sen2α = 1.
Neste caso o seno deve ser igual a 1,
quando 2α = 90º, logo α = 45º
2) No lançamento oblíquo, quando os ângulos de lançamento são complementares as distâncias de alcance horizontal são iguais.
Isto é, por exemplo, os ângulos de lançamento α = 30º e β = 60º são complementares (a soma é igual a 90º). Logo, as distâncias de alcance horizontal são iguais.
Cálculo:
Ilustração: